Difference between revisions of "Inverse Gudermannian"
From specialfunctionswiki
(Created page with "The inverse Gudermannian $\mathrm{gd}^{-1}$ is the inverse function of the Gudermannian function. It may be defined by the following formula for $x \in \mathbb{R}$: $$...") |
|||
| Line 2: | Line 2: | ||
$$\mathrm{gd}^{-1}(x)=\displaystyle\int_0^x \dfrac{1}{\cosh(t)} dt,$$ | $$\mathrm{gd}^{-1}(x)=\displaystyle\int_0^x \dfrac{1}{\cosh(t)} dt,$$ | ||
where $\cosh$ denotes the [[cosh|hyperbolic cosine]]. | where $\cosh$ denotes the [[cosh|hyperbolic cosine]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
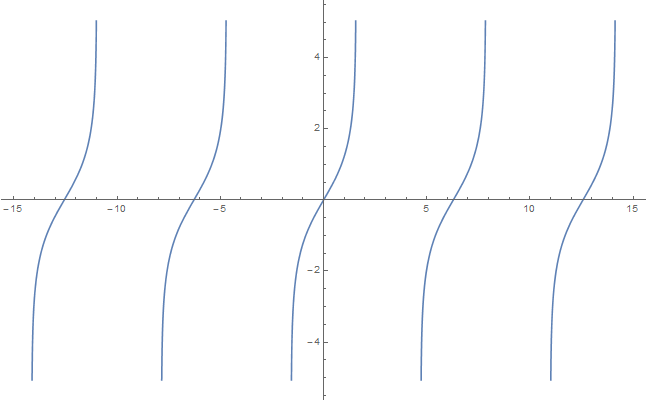
| + | File:Inversegudermannianplot.png|Graph of $\mathrm{gd}^{-1}$. | ||
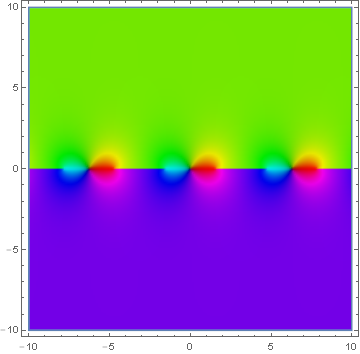
| + | File:Domcolinversegudermannian.png|[[Domain coloring]] of $\mathrm{gd}^{-1}$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
Revision as of 23:21, 25 August 2015
The inverse Gudermannian $\mathrm{gd}^{-1}$ is the inverse function of the Gudermannian function. It may be defined by the following formula for $x \in \mathbb{R}$: $$\mathrm{gd}^{-1}(x)=\displaystyle\int_0^x \dfrac{1}{\cosh(t)} dt,$$ where $\cosh$ denotes the hyperbolic cosine.
Domain coloring of $\mathrm{gd}^{-1}$.