Difference between revisions of "Error function"
(→Properties) |
|||
| Line 4: | Line 4: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
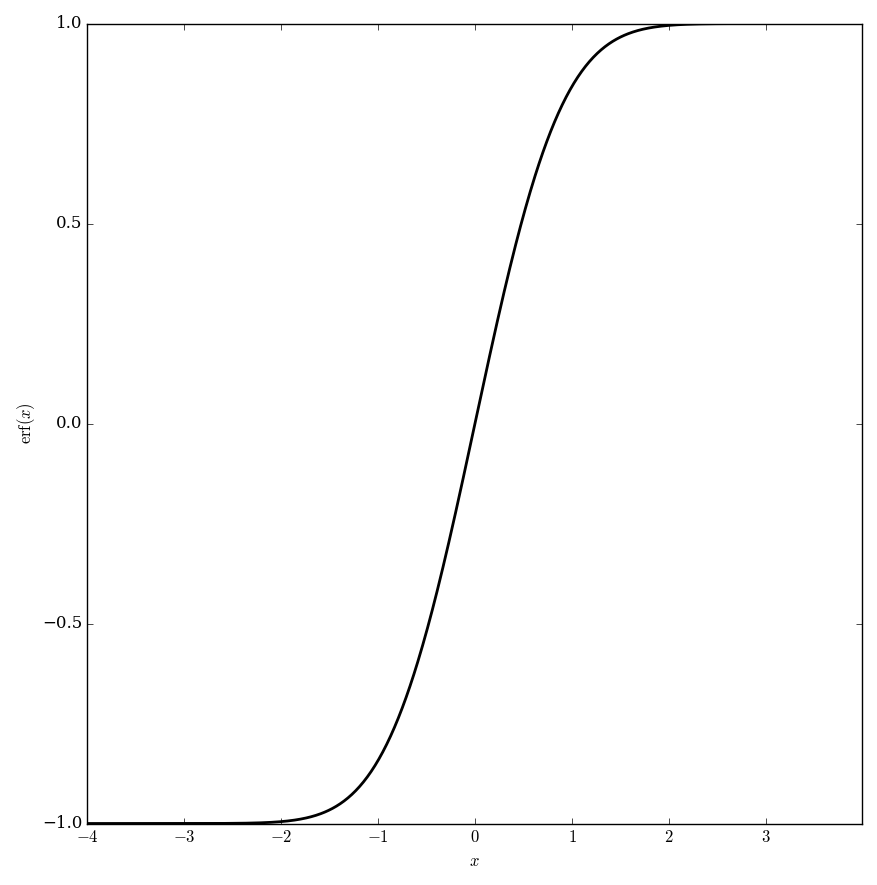
| − | File: | + | File:Erfplot.png|Graph of $\mathrm{erf}$. |
File:Complex erf.png|[[Domain coloring]] of [[analytic continuation]] of $\mathrm{erf}$. | File:Complex erf.png|[[Domain coloring]] of [[analytic continuation]] of $\mathrm{erf}$. | ||
</gallery> | </gallery> | ||
Revision as of 17:23, 23 May 2016
The error function $\mathrm{erf}$ is defined by $$\mathrm{erf}(x)=\dfrac{2}{\sqrt{\pi}}\displaystyle\int_0^x e^{-\tau^2} d\tau.$$
- Complex erf.png
Domain coloring of analytic continuation of $\mathrm{erf}$.
Properties
Theorem: The following formula holds: $\mathrm{erf}(z) = \dfrac{2}{\sqrt{\pi}} \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^kz^{2k+1}}{k!(2k+1)}.$
Proof: █
Theorem: The following formula holds: $\mathrm{erf}(z)=\dfrac{2}{\sqrt{\pi}}e^{-z^2}\displaystyle\sum_{k=0}^{\infty} \dfrac{2^k}{1 \cdot 3 \cdot \ldots \cdot (2k+1)} z^{2k+1}.$
Proof: █
Theorem: The following formula holds:$\mathrm{erf}(-z)=-\mathrm{erf}(z).$
Proof: █
Theorem: The following formula holds:$\mathrm{erf}(\overline{z}) = \overline{\mathrm{erf}}(z).$
Proof: █
Theorem: The following formula holds: $\dfrac{1}{2} \left( 1 + \mathrm{erf} \left( \dfrac{x-\mu}{\sqrt{2}\sigma} \right) \right)=\dfrac{1}{\sigma \sqrt{2 \pi}} \displaystyle\int_{-\infty}^x \exp \left( -\dfrac{(t-\mu)^2}{2\sigma^2} \right)dt.$
Proof: █
Videos
The Laplace transform of the error function $\mathrm{erf}(t)$