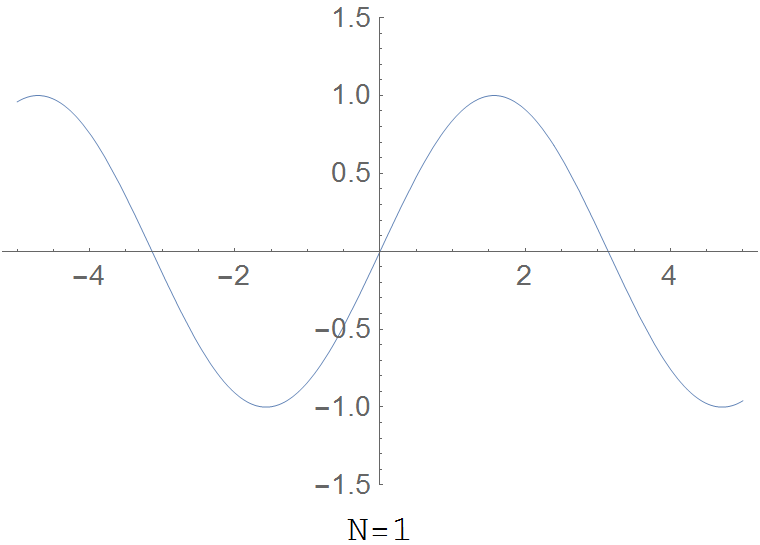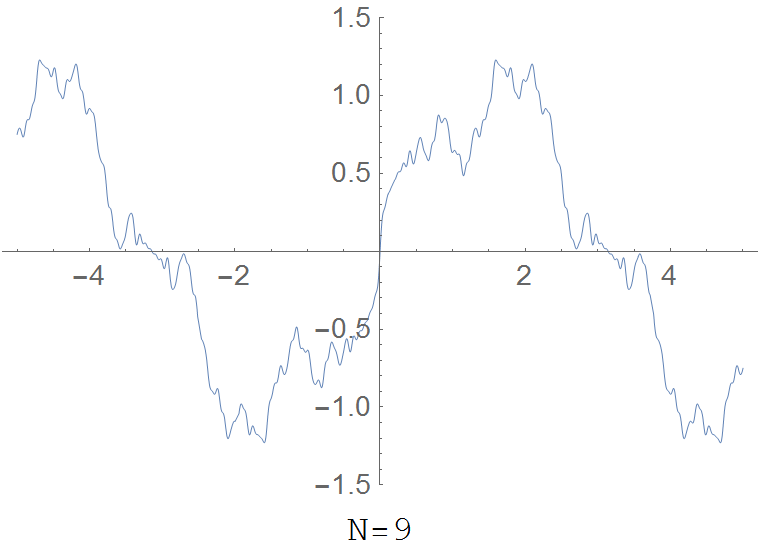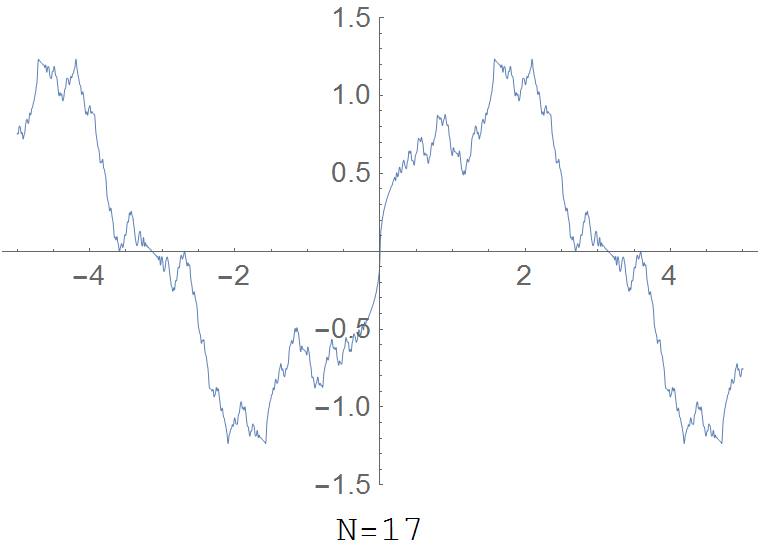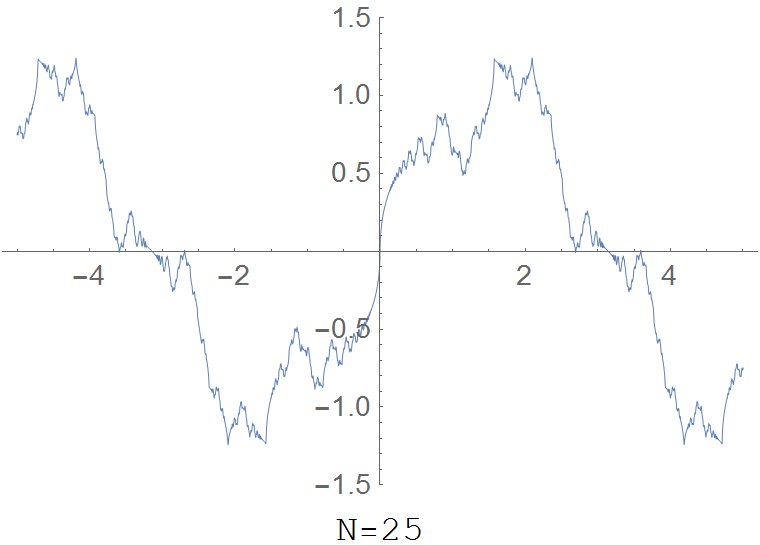Difference between revisions of "Riemann function"
From specialfunctionswiki
| Line 26: | Line 26: | ||
=References= | =References= | ||
[https://pure.ltu.se/ws/files/30923977/LTU-EX-03320-SE.pdf]<br /> | [https://pure.ltu.se/ws/files/30923977/LTU-EX-03320-SE.pdf]<br /> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:34, 24 May 2016
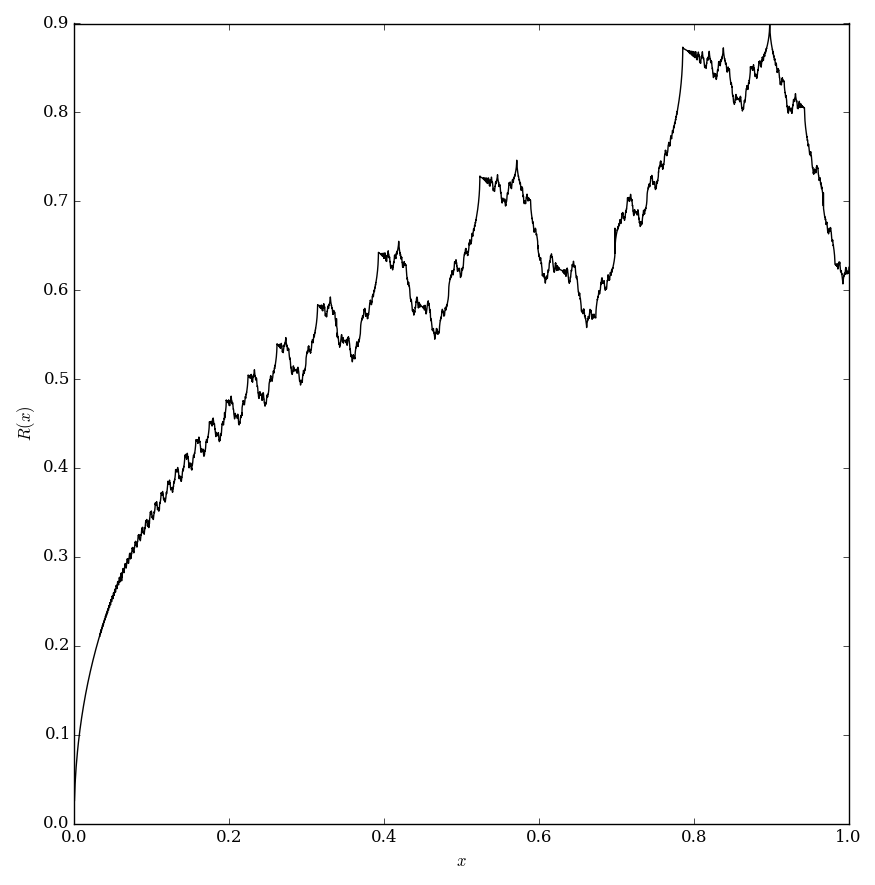
The Riemann function is the function $R \colon \mathbb{R} \rightarrow \mathbb{R}$ defined by $$R(x)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\sin(k^2 x)}{k^2}.$$
Properties
Theorem: The Riemann function is is continuous.
Proof: █
Theorem: The Riemann function is nowhere differentiable except at points of the form $\pi \dfrac{2p+1}{2q+1}$ with $p,q \in \mathbb{Z}$.
Proof: █