Difference between revisions of "Arcsec"
| Line 1: | Line 1: | ||
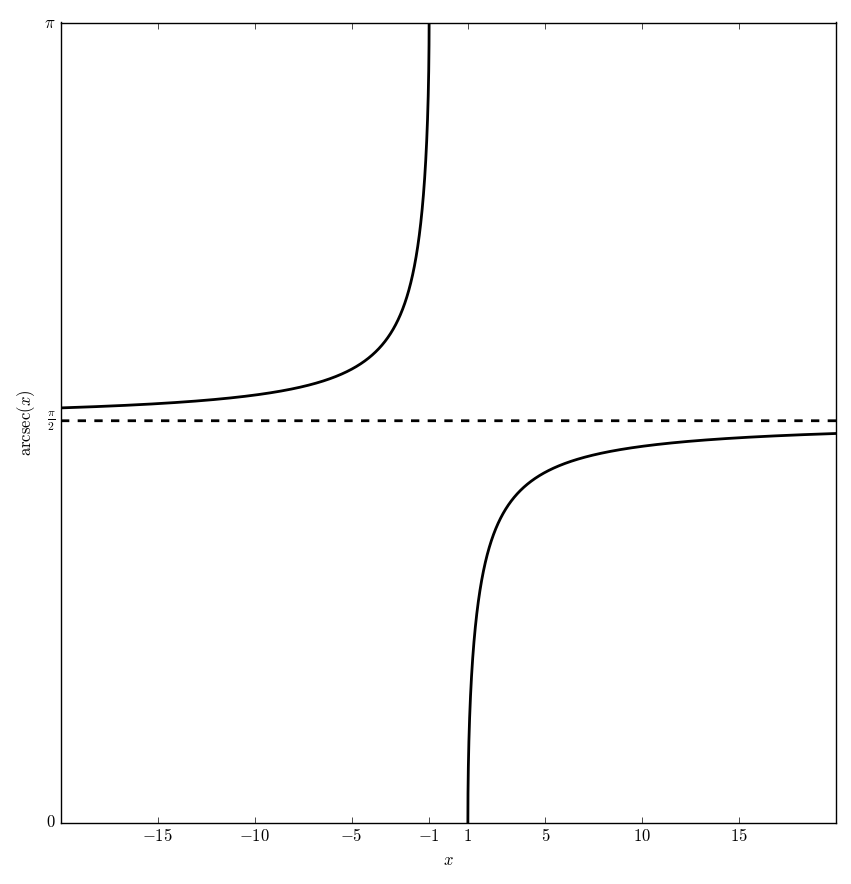
| + | The [[function]] $\mathrm{arcsec} \colon \mathbb{R} \setminus (-1,1) \rightarrow [0,\pi] \setminus \left\{ \dfrac{\pi}{2} \right\}$ is the [[inverse function]] of the [[secant]] function. | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
Revision as of 05:18, 16 May 2016
The function $\mathrm{arcsec} \colon \mathbb{R} \setminus (-1,1) \rightarrow [0,\pi] \setminus \left\{ \dfrac{\pi}{2} \right\}$ is the inverse function of the secant function.
Graph of $\mathrm{arcsec}$.
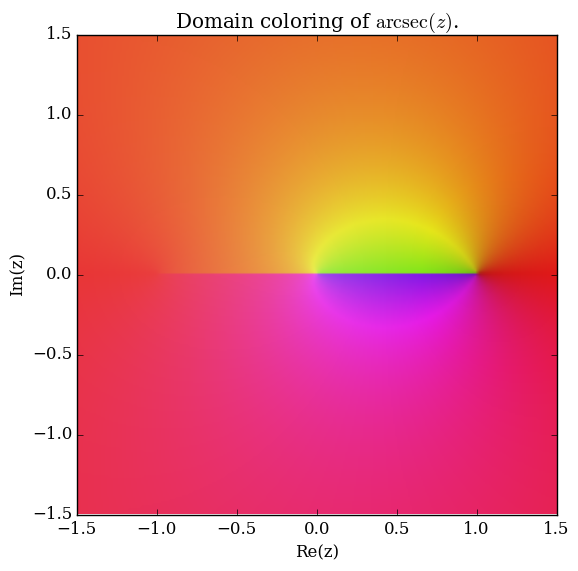
Domain coloring of $\mathrm{arcsec}$.
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arcsec}(z) = \dfrac{1}{z^2\sqrt{1-\frac{1}{z^2}}},$$ where $\mathrm{arcsec}$ is the inverse secant function.
Proof
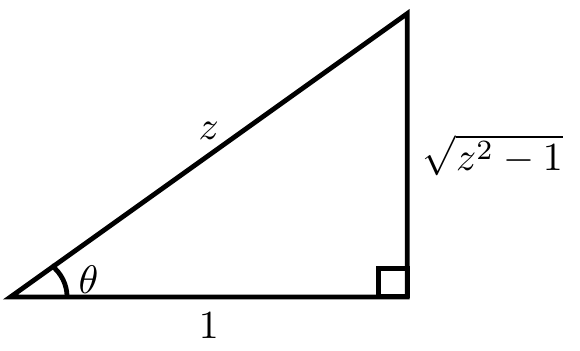
If $\theta=\mathrm{arcsec}(z)$ then $\sec(\theta)=z$. Now use implicit differentiation with respect to $z$ and the derivative of secant to see $$\sec(\theta)\tan(\theta) \theta' = 1,$$ or equivalently, $$\dfrac{\mathrm{d}\theta}{\mathrm{d}z} = \dfrac{1}{\sec(\theta)\tan(\theta)} = \dfrac{1}{z\tan(\theta)}.$$ The following image shows that $\tan(\mathrm{arcsec}(z))=\sqrt{z^2-1}$:
).png)
Hence substituting back in $\theta=\mathrm{arcsec}(z)$ yields the formula $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arcsec}(z) = \dfrac{1}{z\tan(\mathrm{arcsec}(z))} = \dfrac{1}{z\sqrt{z^2-1}}=\dfrac{1}{z^2\sqrt{1-\frac{1}{z^2}}},$$ as was to be shown.
