Difference between revisions of "Sine integral"
From specialfunctionswiki
| Line 20: | Line 20: | ||
<center>{{:*-integral functions footer}}</center> | <center>{{:*-integral functions footer}}</center> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:47, 24 May 2016
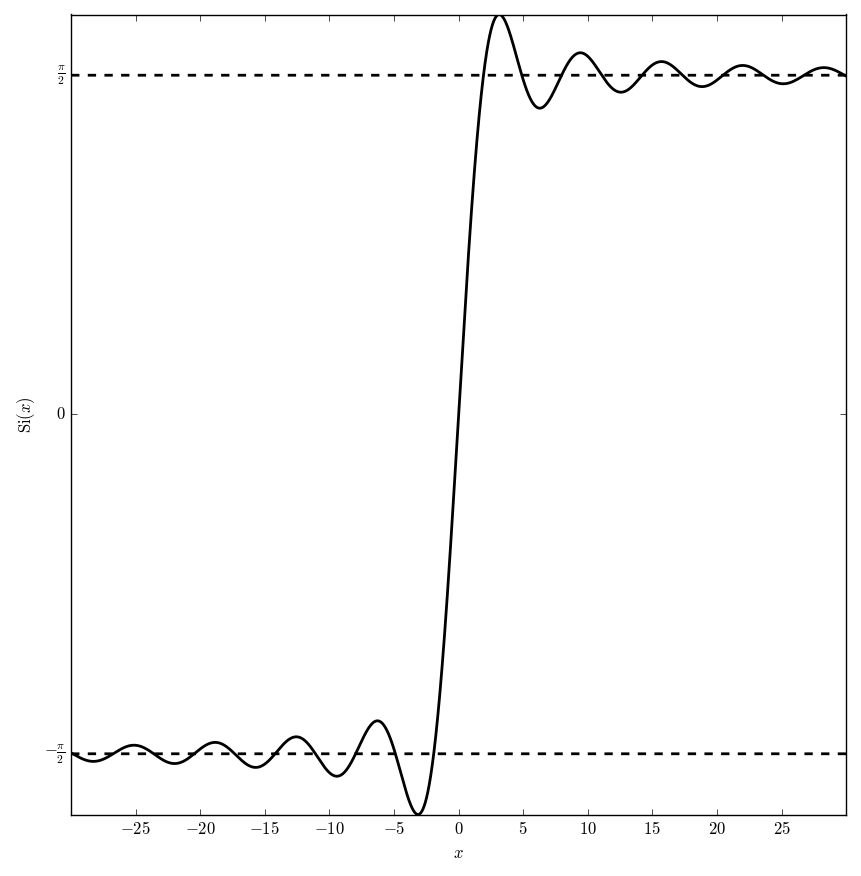
The sine integral is defined by $$\mathrm{Si}(z) = \displaystyle\int_0^z \mathrm{sinc}(t) \mathrm{d}t, \quad |\mathrm{arg} z|<\pi,$$ where $\mathrm{sinc}$ denotes the Sinc function.
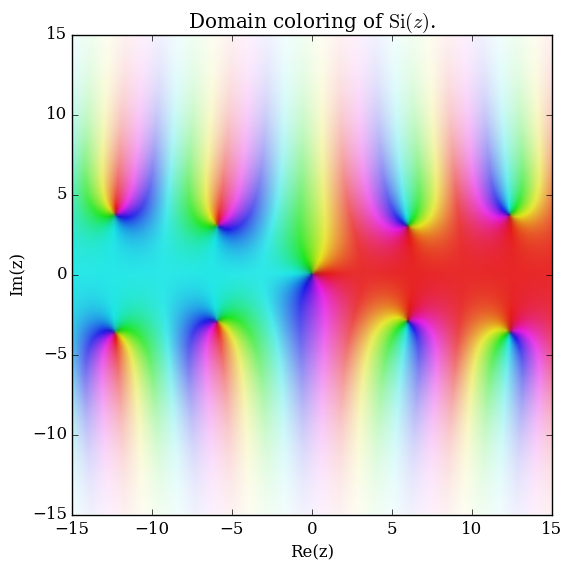
Domain coloring of $\mathrm{Si}$.
Contents
Relationship to other functions
Theorem
The following formula holds: $$\mathrm{Ei}(ix)=\mathrm{Ci}(x)+i\mathrm{Si}(x),$$ where $\mathrm{Ei}$ denotes the exponential integral Ei, $\mathrm{Ci}$ denotes the cosine integral, and $\mathrm{Si}$ denotes the sine integral.
Proof
References
Videos
Laplace Transform of Sine Integral