Difference between revisions of "Fresnel S"
From specialfunctionswiki
| Line 6: | Line 6: | ||
<gallery> | <gallery> | ||
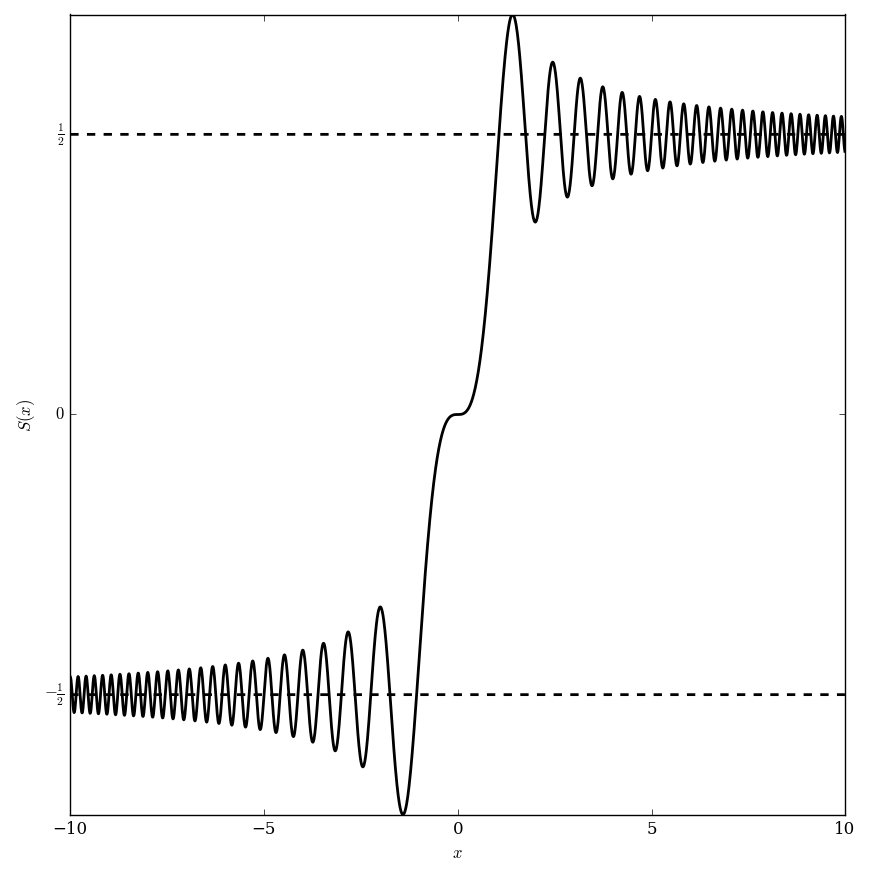
File:Fresnelsplot.png| Graph of $S$. | File:Fresnelsplot.png| Graph of $S$. | ||
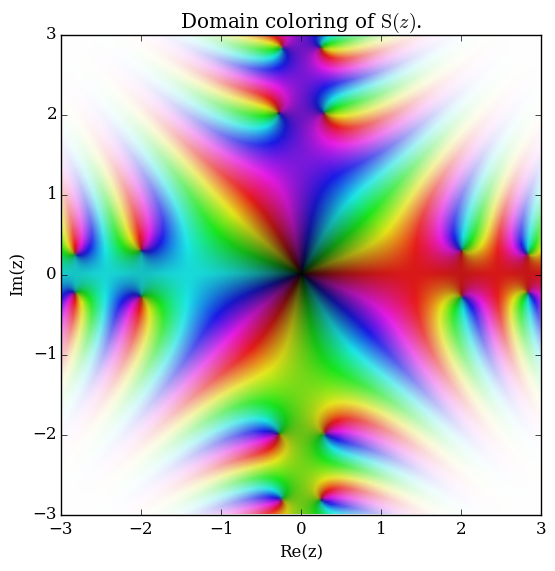
| − | File: | + | File:Complexfresnelsplot.png | [[Domain coloring]] of [[analytic continuation]] of Fresnel $S$. |
</gallery> | </gallery> | ||
</div> | </div> | ||
Revision as of 22:41, 23 May 2016
The Fresnel $S$ function is defined by $$S(z)=\int_0^z \sin(t^2) dt.$$ (Note in Abramowitz&Stegun it is defined differently.)
Domain coloring of analytic continuation of Fresnel $S$.
Properties
Theorem: The following limit is known: $$\displaystyle\lim_{x \rightarrow \infty} S(x) = \displaystyle\int_0^{\infty} \sin(t^2)dt = \sqrt{ \dfrac{\pi}{8}}.$$
Proof: █
See Also
Videos
The Fresnel Integral S(x) - How to integrate sin(x^2)