Difference between revisions of "Chi"
From specialfunctionswiki
| Line 11: | Line 11: | ||
<center>{{:*-integral functions footer}}</center> | <center>{{:*-integral functions footer}}</center> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:47, 24 May 2016
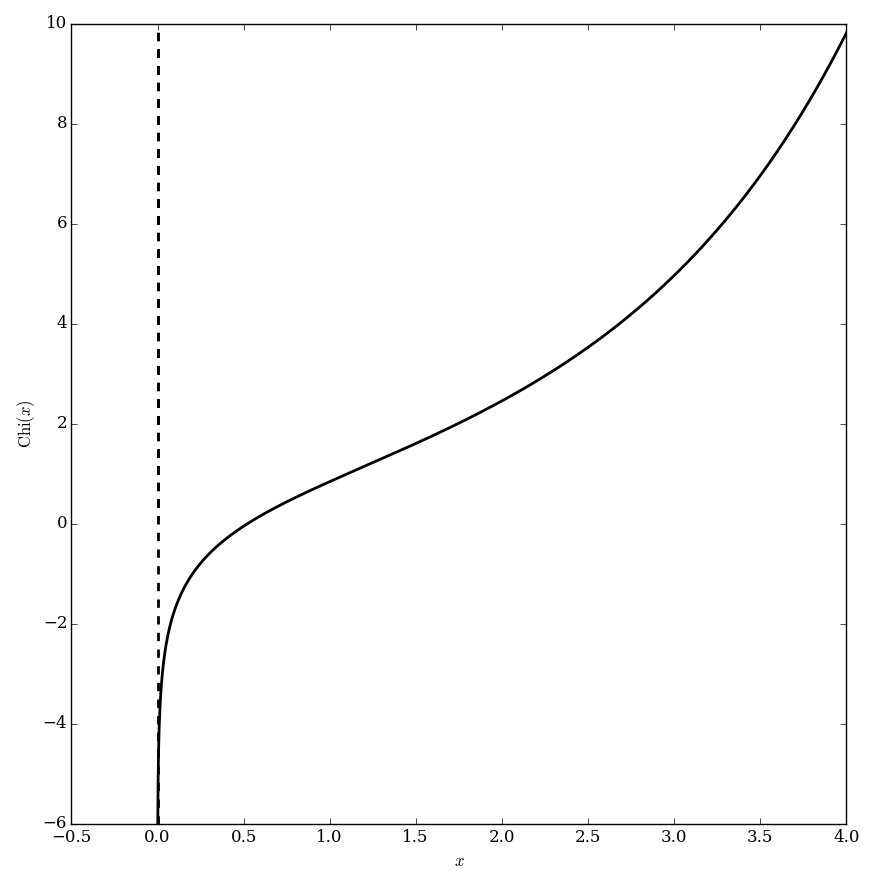
The hyperbolic cosine integral $\mathrm{Chi} \colon (0,\infty) \rightarrow \mathbb{R}$ is defined by the formula $$\mathrm{Chi}(z)=-\displaystyle\int_z^{\infty} \dfrac{\mathrm{cosh}(t)}{t} \mathrm{d}t,$$ where $\cosh$ denotes the hyperbolic cosine.
Graph of $\mathrm{Chi}$.
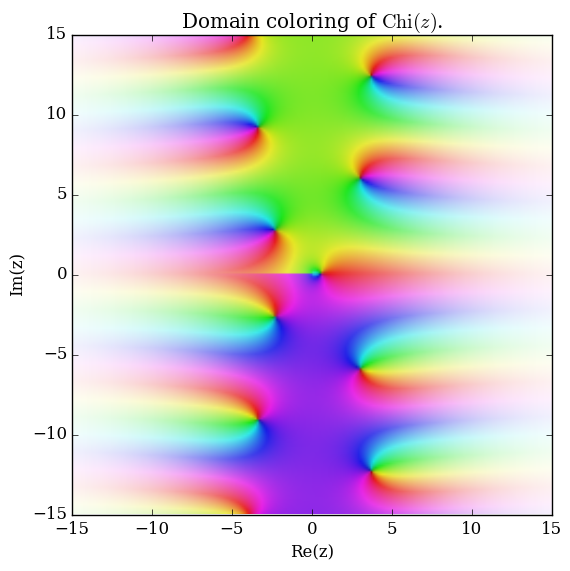
Domain coloring of $\mathrm{Chi}$.
