Difference between revisions of "Bessel J"
| Line 5: | Line 5: | ||
<gallery> | <gallery> | ||
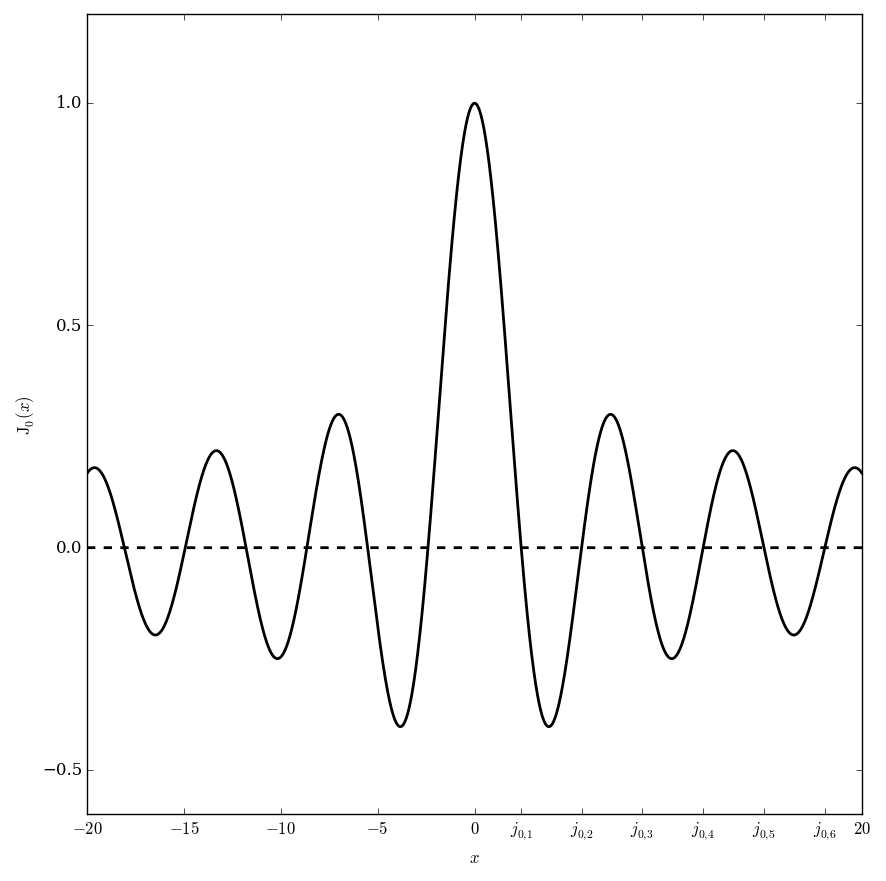
File:Besseljn=0plot.png|Graph of $J_0$. | File:Besseljn=0plot.png|Graph of $J_0$. | ||
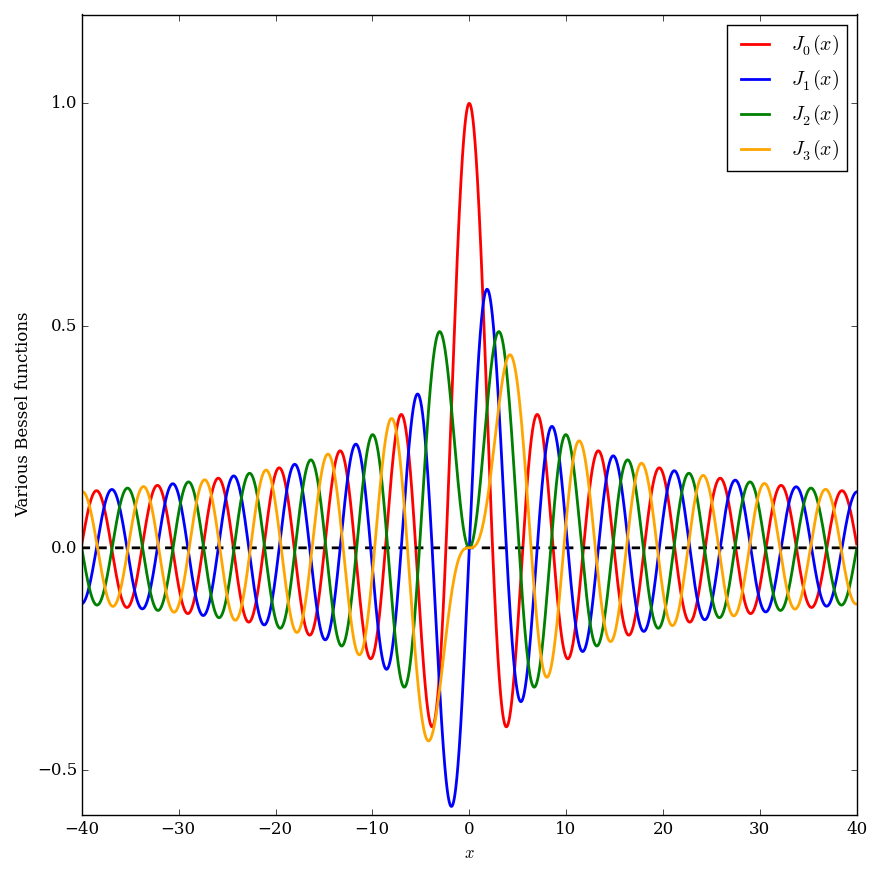
| + | File:Multiplebesseljplot.png|Graph of various Bessel functions. | ||
File:Complexbesselj0.png|[[Domain coloring]] of $J_0$ in $\mathbb{C}$. | File:Complexbesselj0.png|[[Domain coloring]] of $J_0$ in $\mathbb{C}$. | ||
File:Complexbesselj5.png|[[Domain coloring]] of $J_5$ in $\mathbb{C}$. | File:Complexbesselj5.png|[[Domain coloring]] of $J_5$ in $\mathbb{C}$. | ||
Revision as of 06:43, 24 May 2016
The Bessel functions of the first kind, $J_{\nu}$, have a power series expansion $$J_{\nu}(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{k! \Gamma(k+\nu+1)2^{2k+\nu}}z^{2k+\nu}.$$
- Complexbesselj0.png
Domain coloring of $J_0$ in $\mathbb{C}$.
- Complexbesselj5.png
Domain coloring of $J_5$ in $\mathbb{C}$.
Bessel functions from Abramowitz&Stegun
Contents
Properties
Theorem: If $n \in \mathbb{Z}$, then $J_{-n}(x)=(-1)^nJ_n(x)$. Moreover this means that $J_n$ and $J_{-n}$ are linearly dependent.
Proof: █
Theorem: The following formula holds: $$zJ_{\nu}'(z)=\nu J_{\nu}(z) - z J_{\nu+1}(z).$$
Proof: █
Theorem: The following formula holds: $$\dfrac{d}{dz}[z^{-\nu}J_{\nu}(z)] = -z^{-\nu}J_{\nu+1}(z).$$
Proof: █
Theorem: (Generating function) The following formula holds: $$\exp \left( \dfrac{1}{2} z \left( t-\dfrac{1}{t} \right) \right) = \displaystyle\sum_{k=-\infty}^{\infty} t^k J_k(z).$$
Proof: █
Theorem: The following formula holds for $n\in\mathbb{Z}$: $$J_n(z)=\dfrac{1}{\pi} \displaystyle\int_0^{\pi} \cos(n\xi-x\sin(\xi))d\xi.$$
Proof: █
Theorem: The following formula holds for $n>-\frac{1}{2}$: $$J_n(z)=\dfrac{\left(\frac{z}{2}\right)^n}{\sqrt{\pi}\Gamma(n+\frac{1}{2})} \displaystyle\int_{-1}^1 (1-t^2)^{n-\frac{1}{2}}e^{izt}dt.$$
Proof: █
Relations to other special functions
Theorem
The following formula holds: $$y_n\left( \dfrac{1}{ir} \right) = \left(\dfrac{\pi r}{2} \right)^{\frac{1}{2}} e^{ir} \left[ \dfrac{J_{n +\frac{1}{2}}(r)}{i^{n+1}}+i^nJ_{-n-\frac{1}{2}}(r) \right],$$ where $y_n$ denotes a Bessel polynomial and $J_{\nu}$ denotes the Bessel J.
Proof
References
Theorem
The following formula holds: $$J_{n +\frac{1}{2}}(r) = (2\pi r)^{-\frac{1}{2}} \left[\dfrac{e^{ir}}{i^{n+1}} y_n \left( -\dfrac{1}{ir} \right) + i^{n+1}e^{-ir}y_n\left( \dfrac{1}{ir} \right) \right],$$ where $J_{n+\frac{1}{2}}$ denotes a Bessel J, $\pi$ denotes pi, $i$ denotes the imaginary number, $e^{ir}$ denotes the exponential, and $y_n$ denotes a Bessel polynomial.
Proof
References
Theorem
The following formula holds: $$J_{-n-\frac{1}{2}}(r) = (2 \pi r)^{-\frac{1}{2}} \left[ i^n e^{ir} y_n \left( -\dfrac{1}{ir} \right)+ \dfrac{e^{-ir}}{i^n} y_n\left( \dfrac{1}{ir} \right) \right],$$ where $J_{-n-\frac{1}{2}}$ denotes a Bessel function of the first kind and $y_n$ denotes a Bessel polynomial.
Proof
References
Theorem
The following formula holds: $$J_{\nu}(z) = \left( \dfrac{z}{2} \right)^{\nu} \dfrac{1}{\Gamma(\nu+1)} {}_0F_1 \left(-;\nu+1;-\dfrac{z^2}{4} \right),$$ where $J_{\nu}$ denotes the Bessel function of the first kind, $\Gamma$ denotes the gamma function and ${}_0F_1$ denotes the hypergeometric 0F1.
Proof
References
Theorem
The following formula holds for integer $n$: $$\mathbf{J}_n(z)=J_n(z),$$ where $\mathbf{J}_n$ denotes an Anger function and $J_n$ denotes a Bessel function of the first kind.
Proof
References
Videos
Bessel Equation and Bessel functions
Mod-1 Lec-6 Bessel Functions and Their Properties-I
Bessel's Equation by Free Academy
Taylor Series, Bessel, single Variable Calculus, Coursera.org
Ordinary Differential Equations Lecture 7—Bessel functions and the unit step function
Laplace transform of Bessel function order zero
Laplace transform: Integral over Bessel function is one
Orthogonal Properties of Bessel Function, Orthogonal Properties of Bessel Equation
Links
Addition formulas for Bessel functions
Relations between Bessel functions by John D. Cook