Difference between revisions of "Devil's staircase"
From specialfunctionswiki
| Line 10: | Line 10: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Videos= | ||
| + | [https://www.youtube.com/watch?v=sjfgim3hrno Cantor's staircase]<br /> | ||
=References= | =References= | ||
Revision as of 21:11, 1 June 2016
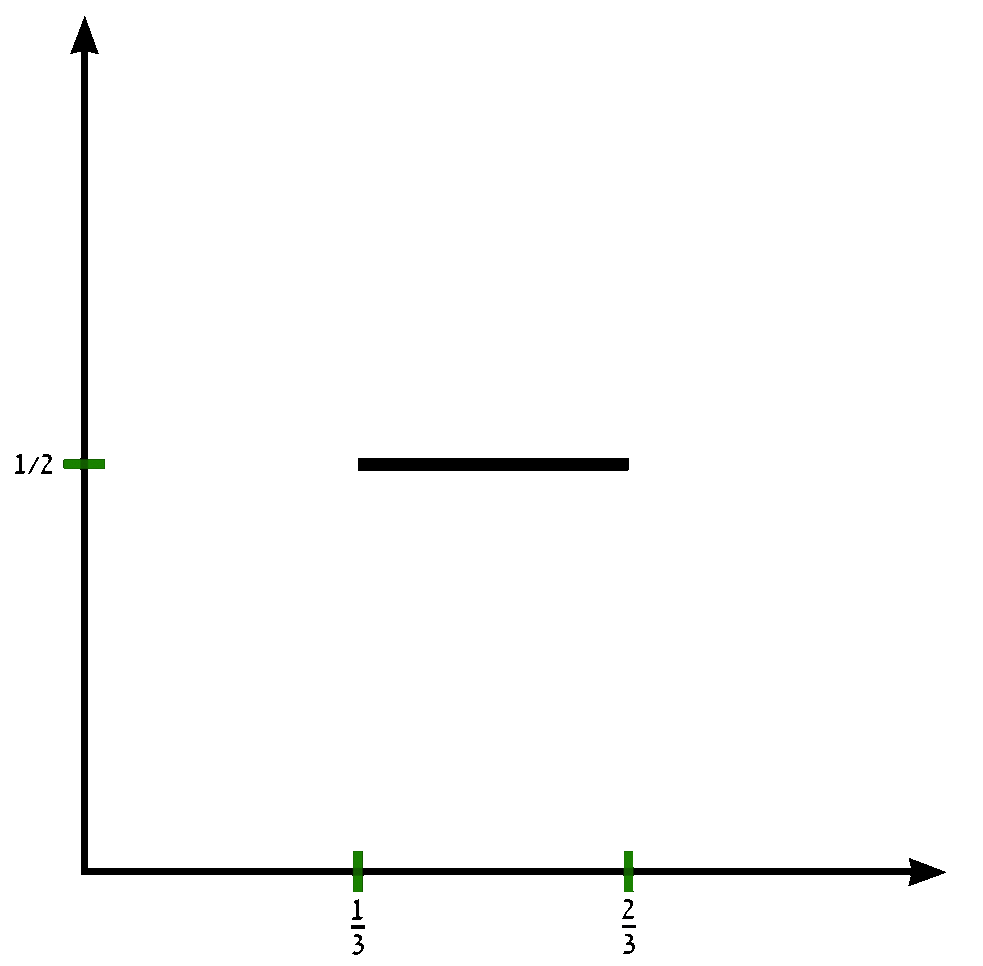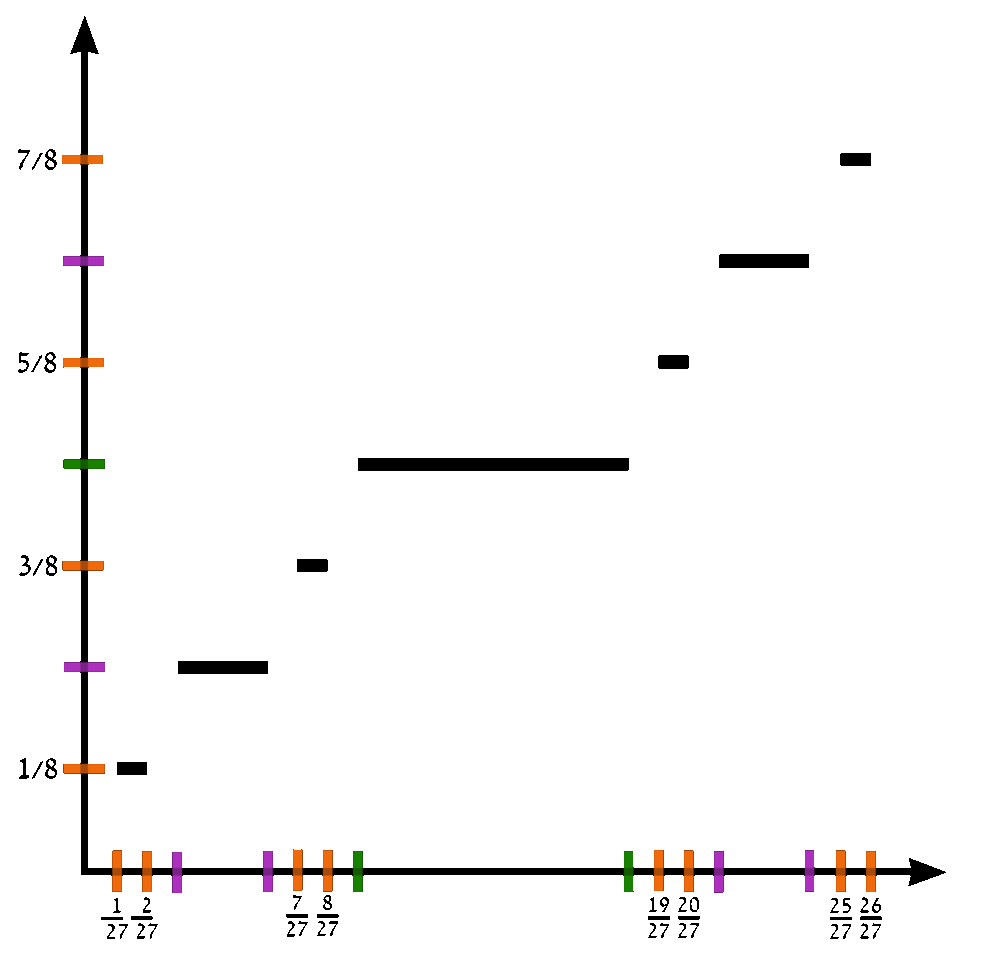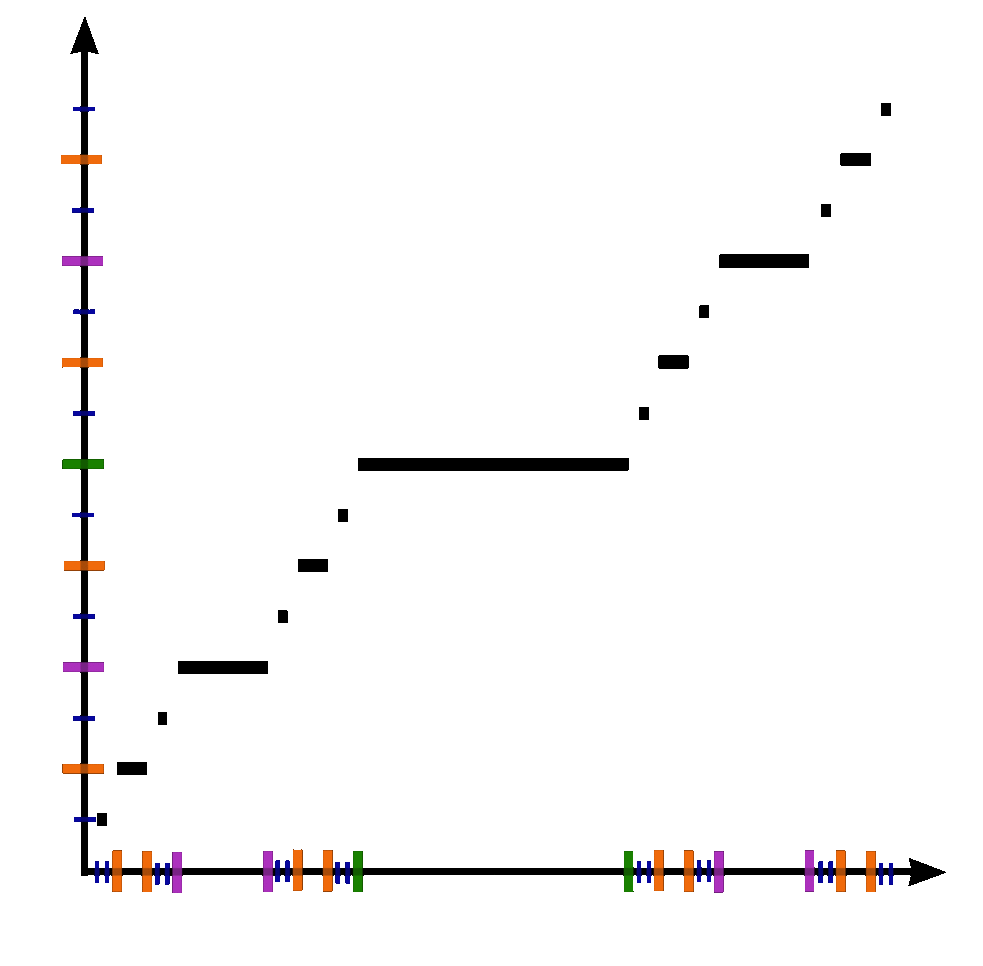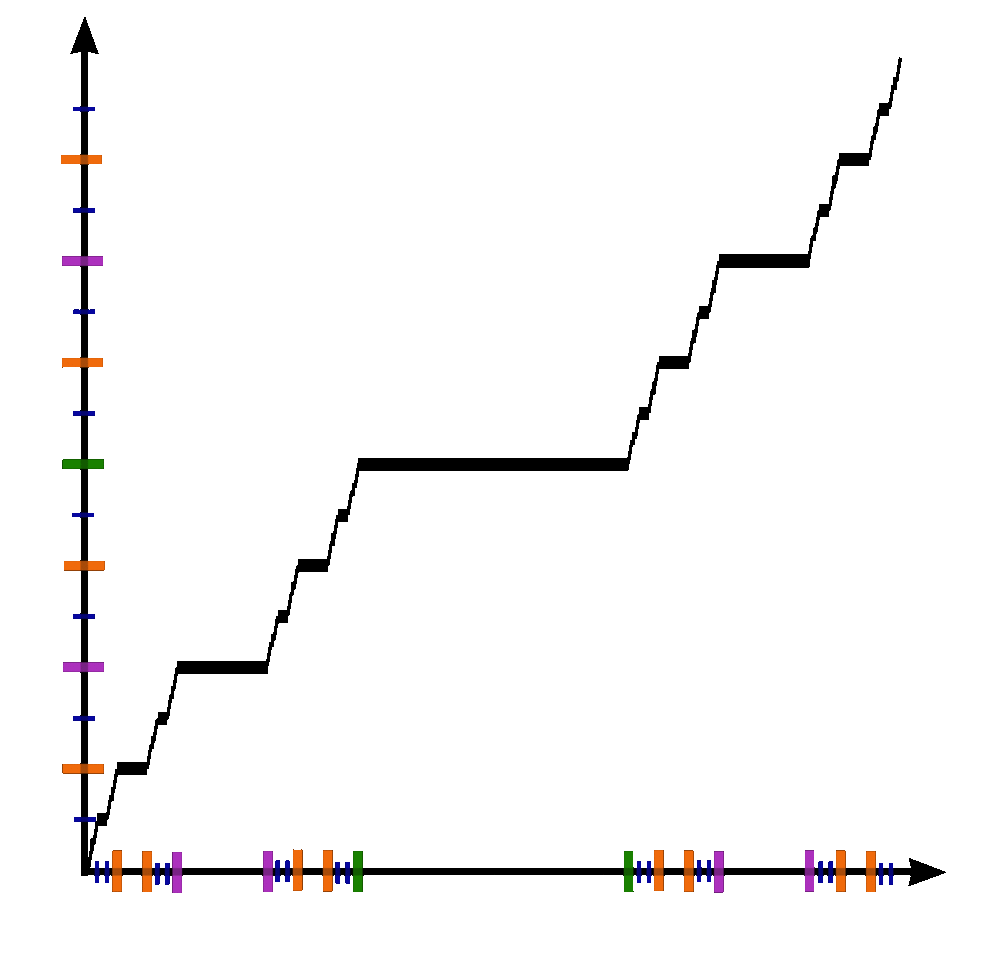
The Devil's staircase, also known as the Cantor function, is a function $c \colon [0,1] \rightarrow [0,1]$ can be expressed by the following rules:
- Write $x$ in base-3.
- If that representation of $x$ contains a $1$, replace every digit after the first $1$ with $0$'s.
- Replace all $2$'s with $1$'s.
- The resulting expansion defines $c(x)$.
Construction of $c$ in steps.
