Difference between revisions of "Faber F2"
From specialfunctionswiki
m (Tom moved page Faber function F2 to Faber F2) |
|
(No difference)
| |
Revision as of 17:16, 23 June 2016
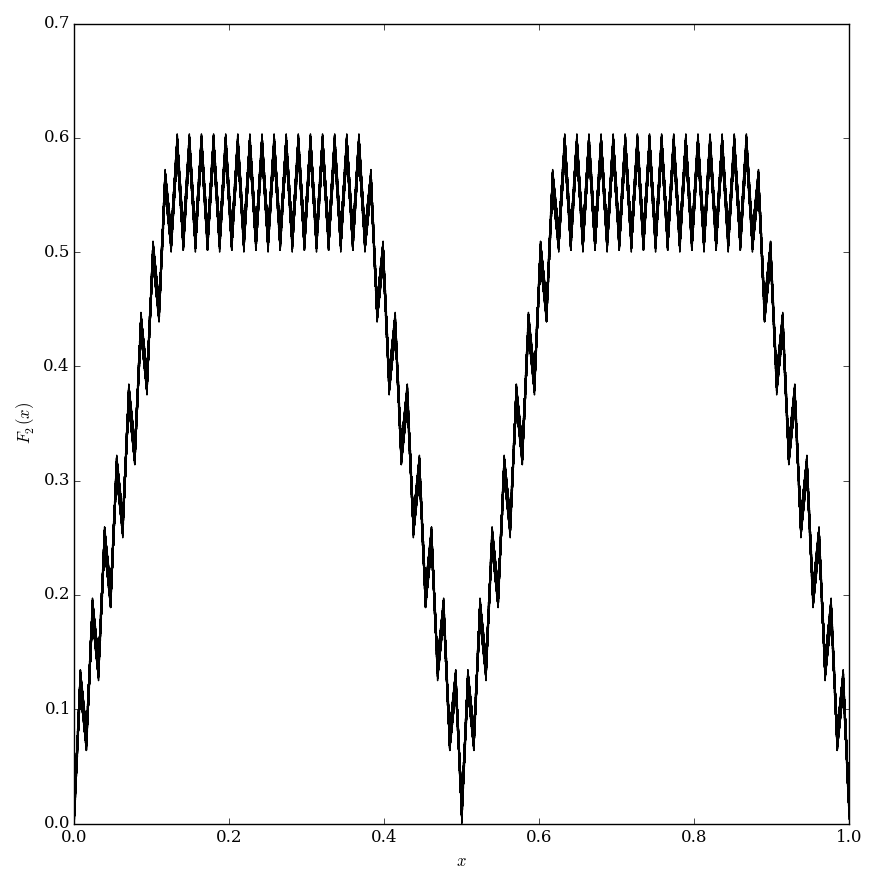
The Faber function $F_2$ is defined by $$F_2(x)=\displaystyle\sum_{k=1}^{\infty} \dfrac{1}{k!} \displaystyle\inf_{m \in \mathbb{Z}} \left|2^{k!}x-m \right|.$$
Graph of $F_2$.
Properties
Theorem: The Faber function $F_2$ is continuous.
Proof: █
Theorem: The Faber function $F_2$ is nowhere differentiable.
Proof: █
