Difference between revisions of "Sech"
| Line 1: | Line 1: | ||
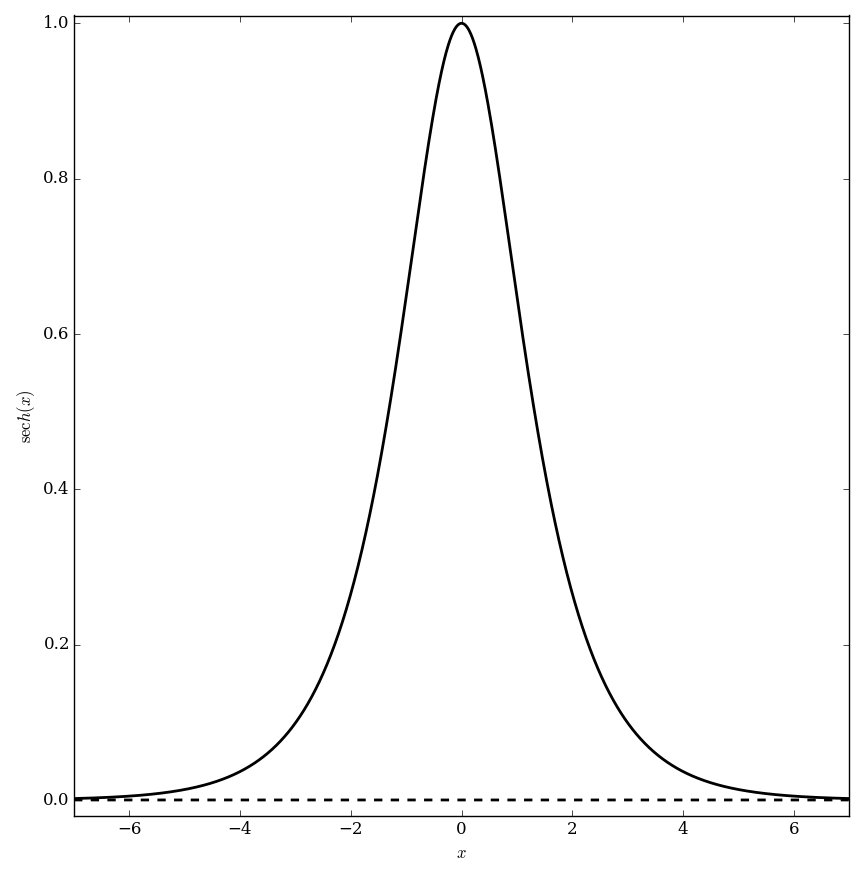
The hyperbolic secant function $\mathrm{sech} \colon \mathbb{R} \rightarrow (0,1]$ is defined by | The hyperbolic secant function $\mathrm{sech} \colon \mathbb{R} \rightarrow (0,1]$ is defined by | ||
$$\mathrm{sech}(z)=\dfrac{1}{\cosh(z)}.$$ | $$\mathrm{sech}(z)=\dfrac{1}{\cosh(z)}.$$ | ||
| − | Since this function is not [[one-to-one]], we define the [[arcsech|inverse hyperbolic secant function]] | + | Since this function is not [[one-to-one]], we define the [[arcsech|inverse hyperbolic secant function]] as the [[inverse function]] of $\mathrm{sech}$ restricted to $[0,\infty)$. |
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
Revision as of 22:16, 24 May 2016
The hyperbolic secant function $\mathrm{sech} \colon \mathbb{R} \rightarrow (0,1]$ is defined by $$\mathrm{sech}(z)=\dfrac{1}{\cosh(z)}.$$ Since this function is not one-to-one, we define the inverse hyperbolic secant function as the inverse function of $\mathrm{sech}$ restricted to $[0,\infty)$.
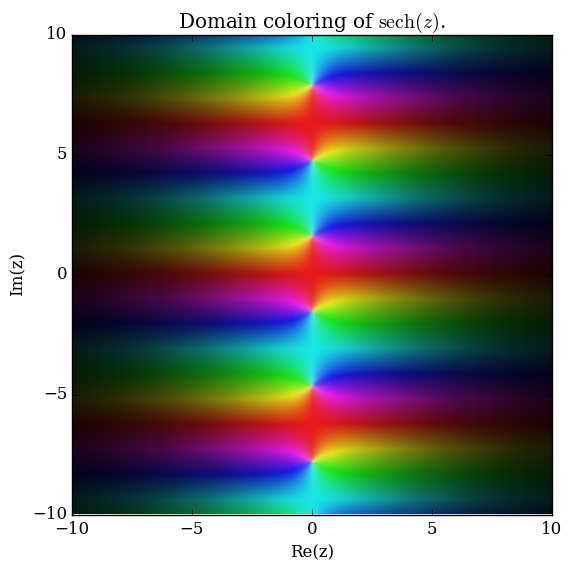
Domain coloring of analytic continuation of $\mathrm{sech}$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{sech}(z)=-\mathrm{sech}(z)\mathrm{tanh}(z),$$ where $\mathrm{sech}$ denotes the hyperbolic secant and $\mathrm{tanh}$ denotes the hyperbolic tangent.
Proof
From the definition, $$\mathrm{sech}(z) = \dfrac{1}{\mathrm{cosh}(z)}.$$ Using the quotient rule, the derivative of cosh, and the definition of $\mathrm{tanh}$, we see $$\begin{array}{ll} \dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{sech}(z) &= \dfrac{0-\sinh(z)}{\cosh(z)^2} \\ &=-\mathrm{sech}(z)\mathrm{tanh}(z), \end{array}$$ as was to be shown.
References
Theorem
The following formula holds: $$\displaystyle\int \mathrm{sech}(z) \mathrm{d}z=\arctan(\sinh(z)) + C,$$ where $\mathrm{sech}$ denotes the hyperbolic secant, $\arctan$ denotes the inverse tangent, and $\sinh$ denotes the hyperbolic sine.
Proof
References
Theorem
The following formula holds: $$\cos(\mathrm{gd}(x))=\mathrm{sech}(x),$$ where $\cos$ denotes the cosine, $\mathrm{gd}$ denotes the Gudermannian, and $\mathrm{sech}$ denotes the hyperbolic secant.
Proof
References
Theorem
The following formula holds: $$\mathrm{sech}(\mathrm{gd}^{-1}(x))=\cos(x),$$ where $\mathrm{sech}$ is the hyperbolic secant, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\cos$ is the cosine.