Difference between revisions of "Csch"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
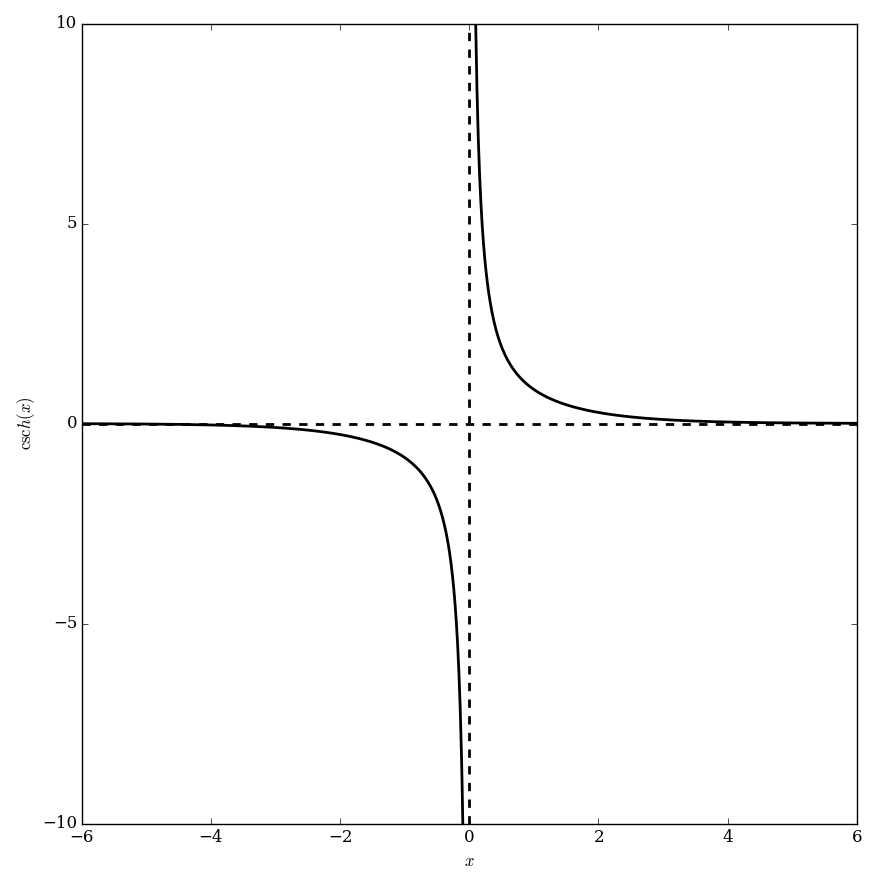
The hyperbolic cosecant function $\mathrm{csch} \colon \mathbb{R} \setminus \{0\} \rightarrow \mathbb{R} \setminus \{0\}$ is defined by | The hyperbolic cosecant function $\mathrm{csch} \colon \mathbb{R} \setminus \{0\} \rightarrow \mathbb{R} \setminus \{0\}$ is defined by | ||
$$\mathrm{csch}(z)=\dfrac{1}{\sinh(z)},$$ | $$\mathrm{csch}(z)=\dfrac{1}{\sinh(z)},$$ | ||
| Line 11: | Line 12: | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of hyperbolic cosecant]]<br /> | |
| − | + | [[Antiderivative of hyperbolic cosecant]]<br /> | |
| − | + | [[Relationship between cot, Gudermannian, and csch]]<br /> | |
| − | + | [[Relationship between csch, inverse Gudermannian, and cot]]<br /> | |
=See Also= | =See Also= | ||
Revision as of 07:51, 8 June 2016
The hyperbolic cosecant function $\mathrm{csch} \colon \mathbb{R} \setminus \{0\} \rightarrow \mathbb{R} \setminus \{0\}$ is defined by $$\mathrm{csch}(z)=\dfrac{1}{\sinh(z)},$$ where $\sinh$ denotes the hyperbolic sine. Since this function is one-to-one, its inverse function, the inverse hyperbolic cosecant function is clear.
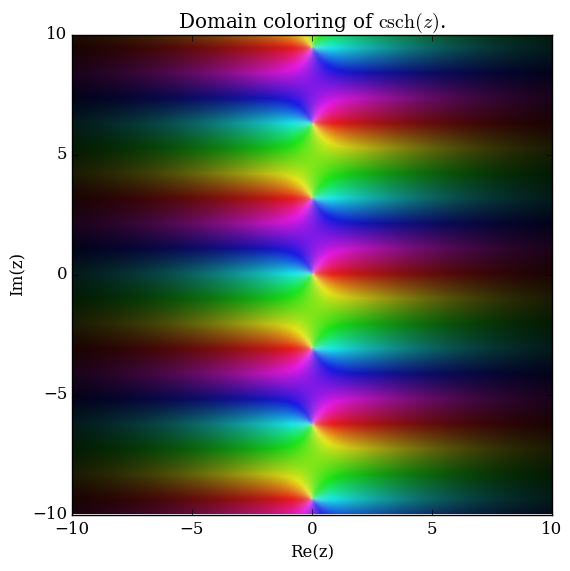
Domain coloring of analytic continuation of $\mathrm{csch}$.
Properties
Derivative of hyperbolic cosecant
Antiderivative of hyperbolic cosecant
Relationship between cot, Gudermannian, and csch
Relationship between csch, inverse Gudermannian, and cot