Difference between revisions of "Exponential integral Ei"
From specialfunctionswiki
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
| − | + | [[Relationship between logarithmic integral and exponential integral]]<br /> | |
| − | + | [[Exponential integral Ei series]]<br /> | |
| − | + | [[Relationship between exponential integral Ei, cosine integral, and sine integral]]<br /> | |
| − | |||
| − | |||
=References= | =References= | ||
Revision as of 08:04, 8 June 2016
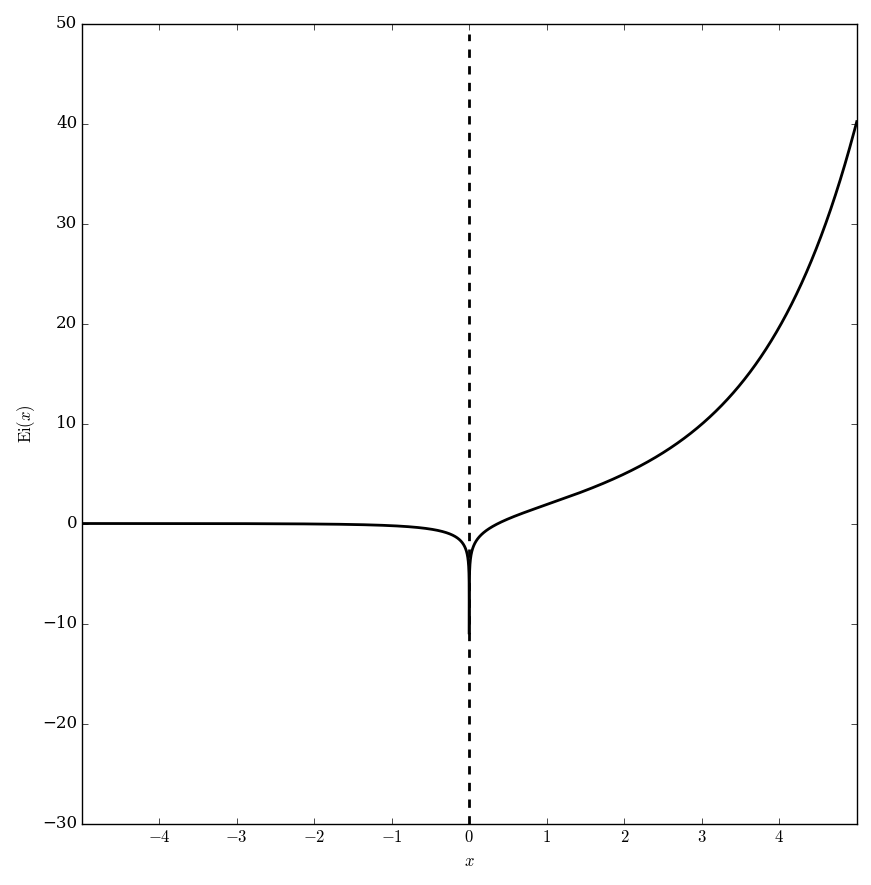
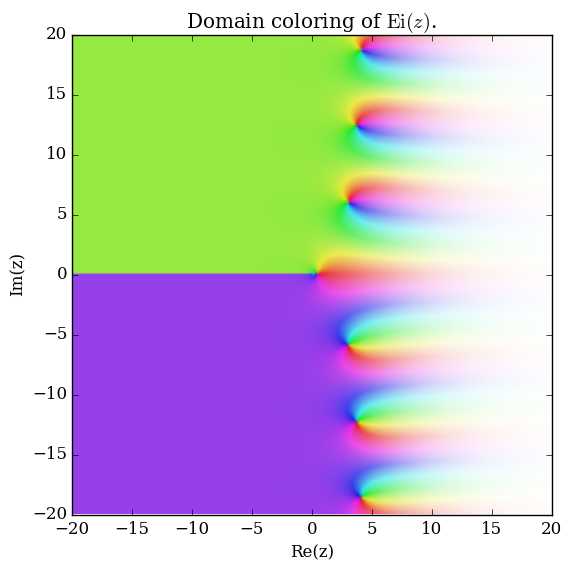
The exponential integral $\mathrm{Ei}$ is defined by $$\mathrm{Ei}(z) = \int_{-\infty}^x \dfrac{e^t}{t} \mathrm{d}t, \quad \left|\mathrm{arg}(-z) \right|<\pi.$$
Properties
Relationship between logarithmic integral and exponential integral
Exponential integral Ei series
Relationship between exponential integral Ei, cosine integral, and sine integral
References
Exponential Integral and Related Functions
On certain definite integrals involving the exponential-integral - J.W.L. Glaisher