Difference between revisions of "Polygamma"
From specialfunctionswiki
| Line 2: | Line 2: | ||
$$\psi^{(m)}(z) = \dfrac{d^m}{dz^m} \log \Gamma(z),$$ | $$\psi^{(m)}(z) = \dfrac{d^m}{dz^m} \log \Gamma(z),$$ | ||
where $\log$ denotes the [[logarithm]] and $\log \Gamma$ denotes the [[loggamma]] function. The [[digamma]] function $\psi$ is the function $\psi^{(0)}(z)$ and the [[trigamma]] function is $\psi^{(1)}(z)$. | where $\log$ denotes the [[logarithm]] and $\log \Gamma$ denotes the [[loggamma]] function. The [[digamma]] function $\psi$ is the function $\psi^{(0)}(z)$ and the [[trigamma]] function is $\psi^{(1)}(z)$. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
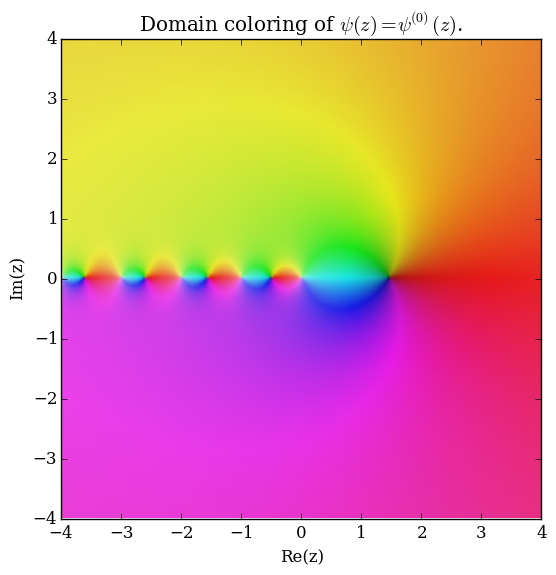
| + | File:Complexdigammaplot.png|Domain coloring of $\psi^{(0)}(z)$. | ||
| + | </gallery> | ||
| + | </div> | ||
=See Also= | =See Also= | ||
Revision as of 18:49, 3 June 2016
The polygamma function of order $m$, $\psi^{(m)}(z)$, is defined by the formula $$\psi^{(m)}(z) = \dfrac{d^m}{dz^m} \log \Gamma(z),$$ where $\log$ denotes the logarithm and $\log \Gamma$ denotes the loggamma function. The digamma function $\psi$ is the function $\psi^{(0)}(z)$ and the trigamma function is $\psi^{(1)}(z)$.