Difference between revisions of "Polygamma"
From specialfunctionswiki
| Line 1: | Line 1: | ||
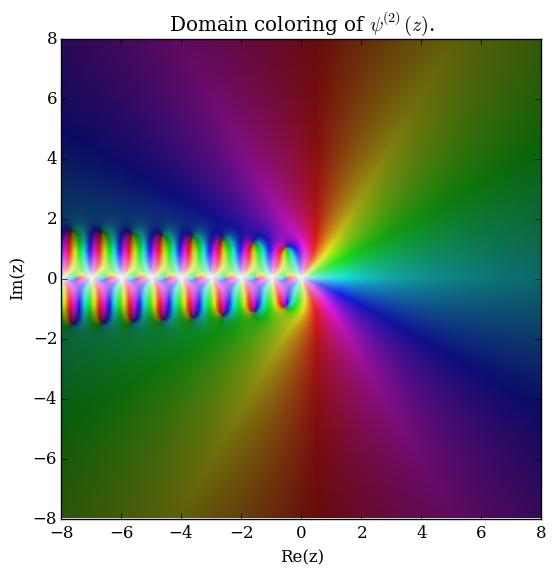
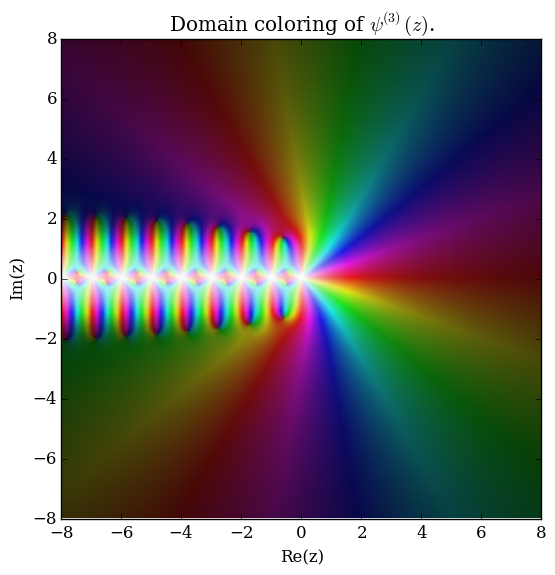
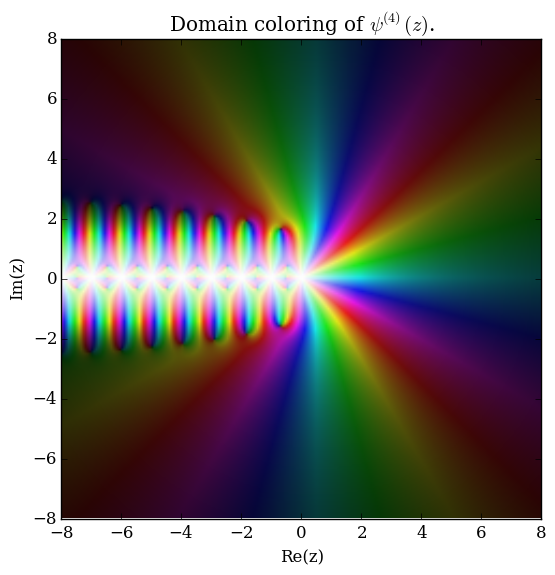
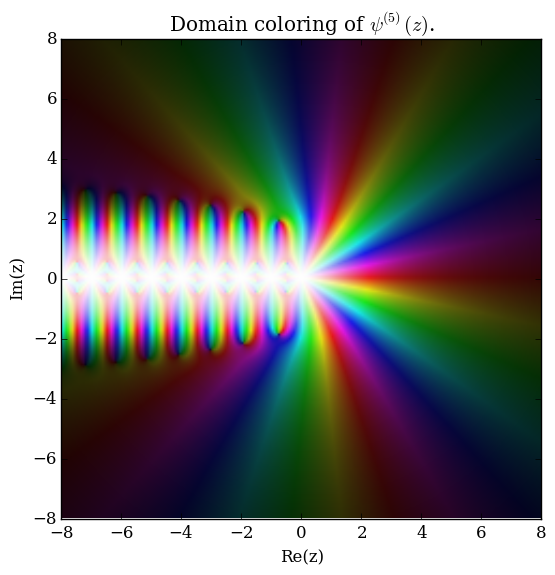
The polygamma function of order $m$, $\psi^{(m)}(z)$, is defined by the formula | The polygamma function of order $m$, $\psi^{(m)}(z)$, is defined by the formula | ||
| − | $$\psi^{(m)}(z) = \dfrac{d^m}{ | + | $$\psi^{(m)}(z) = \dfrac{\mathrm{d}^{m+1}}{\mathrm{d}z^{m+1}} \log \Gamma(z),$$ |
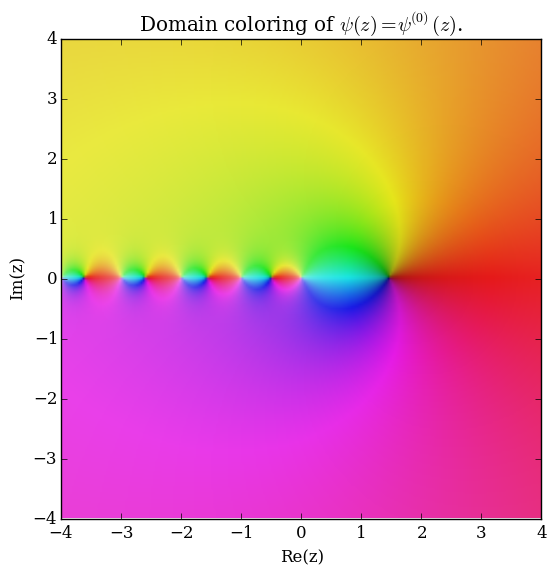
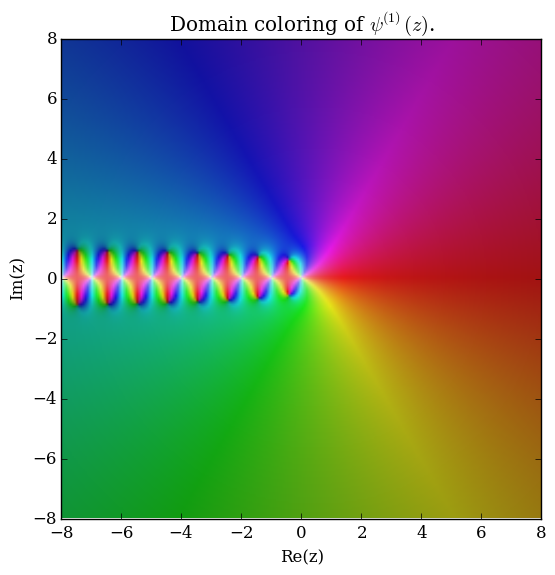
where $\log$ denotes the [[logarithm]] and $\log \Gamma$ denotes the [[loggamma]] function. The [[digamma]] function $\psi$ is the function $\psi^{(0)}(z)$ and the [[trigamma]] function is $\psi^{(1)}(z)$. | where $\log$ denotes the [[logarithm]] and $\log \Gamma$ denotes the [[loggamma]] function. The [[digamma]] function $\psi$ is the function $\psi^{(0)}(z)$ and the [[trigamma]] function is $\psi^{(1)}(z)$. | ||
Revision as of 19:15, 3 June 2016
The polygamma function of order $m$, $\psi^{(m)}(z)$, is defined by the formula $$\psi^{(m)}(z) = \dfrac{\mathrm{d}^{m+1}}{\mathrm{d}z^{m+1}} \log \Gamma(z),$$ where $\log$ denotes the logarithm and $\log \Gamma$ denotes the loggamma function. The digamma function $\psi$ is the function $\psi^{(0)}(z)$ and the trigamma function is $\psi^{(1)}(z)$.
Domain coloring of $\psi^{(0)}(z)$.
Domain coloring of $\psi^{(1)}(z)$.
Domain coloring of $\psi^{(2)}(z)$.
Domain coloring of $\psi^{(3)}(z)$.
Domain coloring of $\psi^{(4)}(z)$.
Domain coloring of $\psi^{(5)}(z)$.
