Difference between revisions of "Anger function"
From specialfunctionswiki
(→Properties) |
|||
| Line 1: | Line 1: | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
| − | The Anger function is defined by | + | Let $\nu \in \mathbb{C}$. The Anger function $\mathbf{J}_{\nu}$ is defined by |
$$\mathbf{J}_{\nu}(z) = \dfrac{1}{\pi} \displaystyle\int_0^{\pi} \cos(\nu \theta - z \sin(\theta)) \mathrm{d}\theta.$$ | $$\mathbf{J}_{\nu}(z) = \dfrac{1}{\pi} \displaystyle\int_0^{\pi} \cos(\nu \theta - z \sin(\theta)) \mathrm{d}\theta.$$ | ||
| Line 26: | Line 26: | ||
=See Also= | =See Also= | ||
[[Bessel J]]<br /> | [[Bessel J]]<br /> | ||
| − | [[Weber function]] | + | [[Weber function]]<br /> |
=References= | =References= | ||
| − | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Relationship between modified Struve L and modified spherical Bessel j functions|next=Anger of integer order is Bessel J}}:12.3.1 | |
Revision as of 04:04, 6 June 2016
Let $\nu \in \mathbb{C}$. The Anger function $\mathbf{J}_{\nu}$ is defined by $$\mathbf{J}_{\nu}(z) = \dfrac{1}{\pi} \displaystyle\int_0^{\pi} \cos(\nu \theta - z \sin(\theta)) \mathrm{d}\theta.$$
Graph of $\mathbf{J}_0$.
Graph of $\mathbf{J}_{\frac{1}{2}}$.
Graph of $\mathbf{J}_{\frac{3}{2}}$.
Graph of $\mathbf{J}_2$.
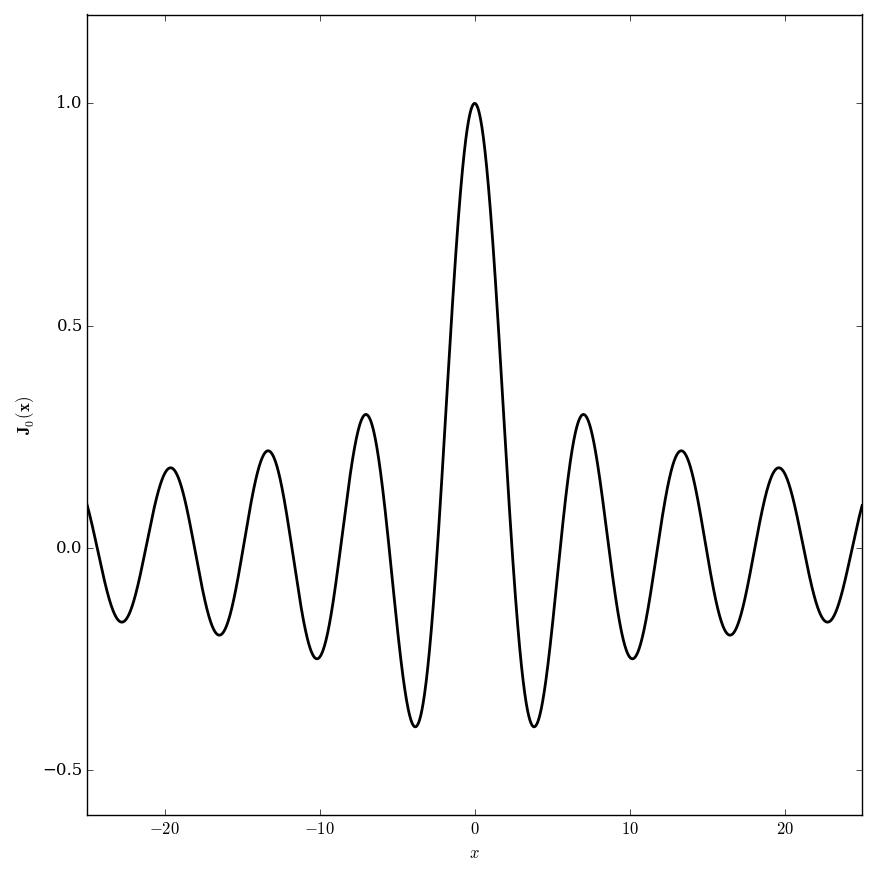
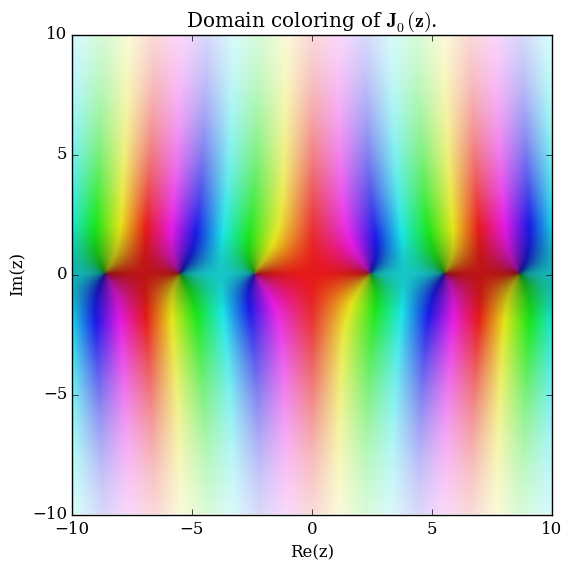
Domain coloring of $\mathbf{J}_0$.
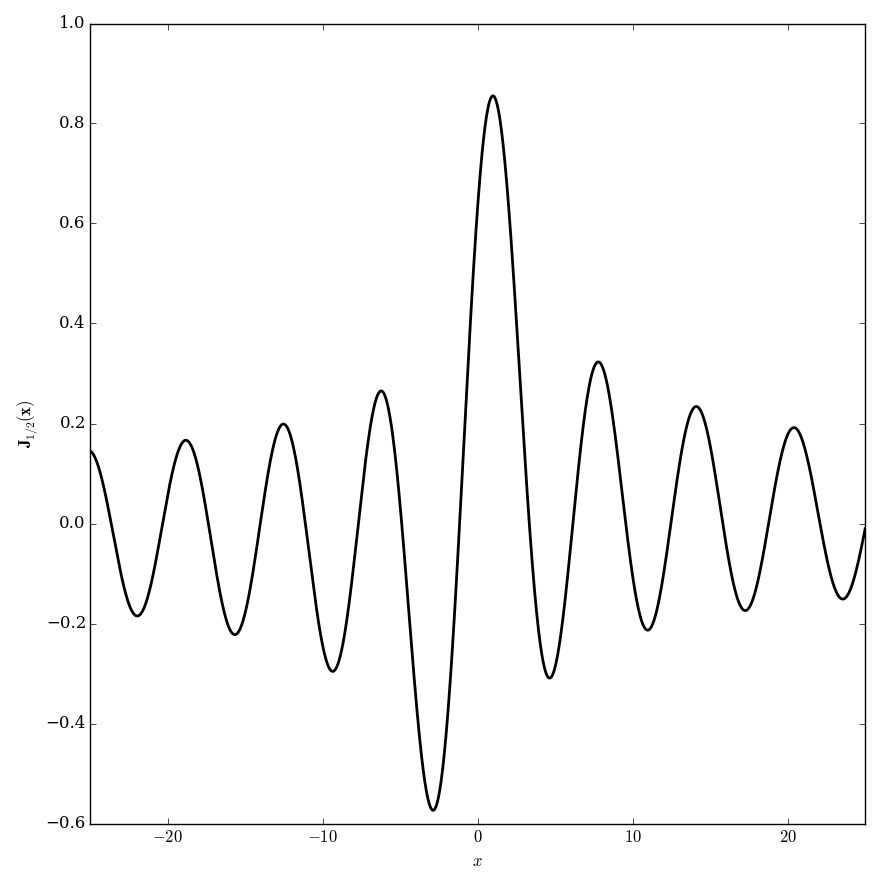
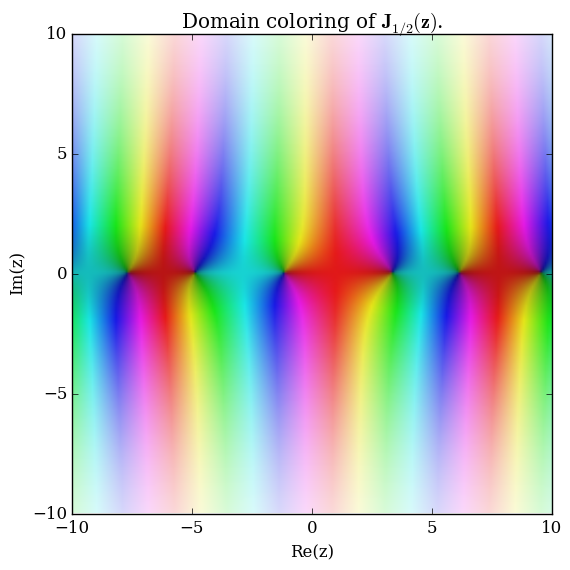
Domain coloring of $\mathbf{J}_{\frac{1}{2}}$.
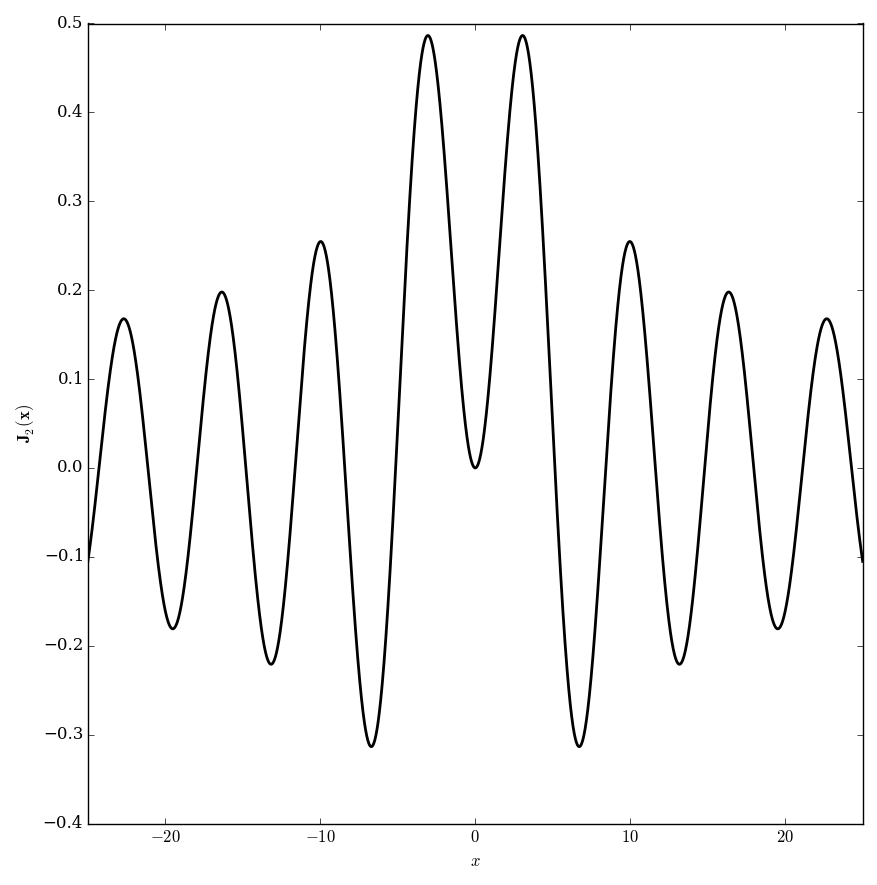
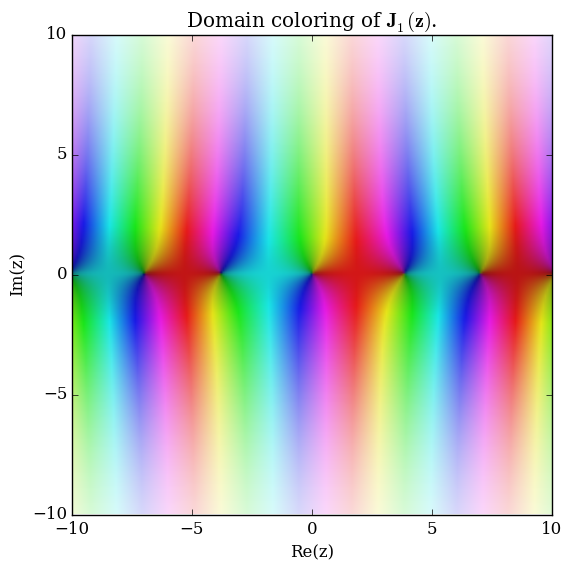
Domain coloring of $\mathbf{J}_1$.
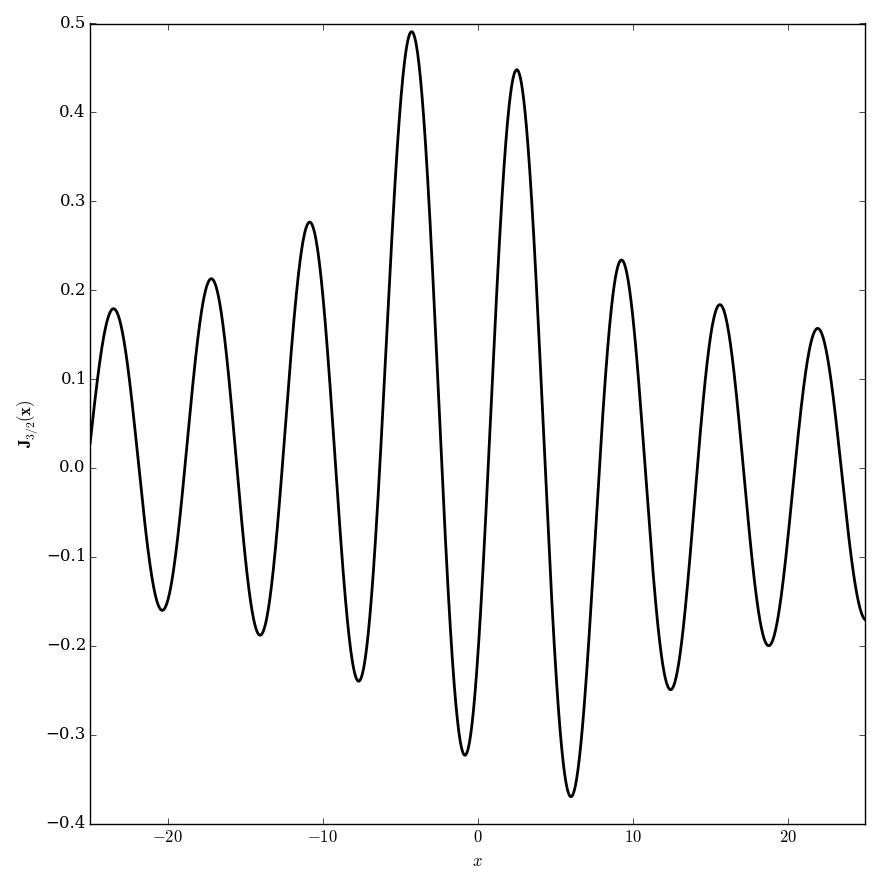
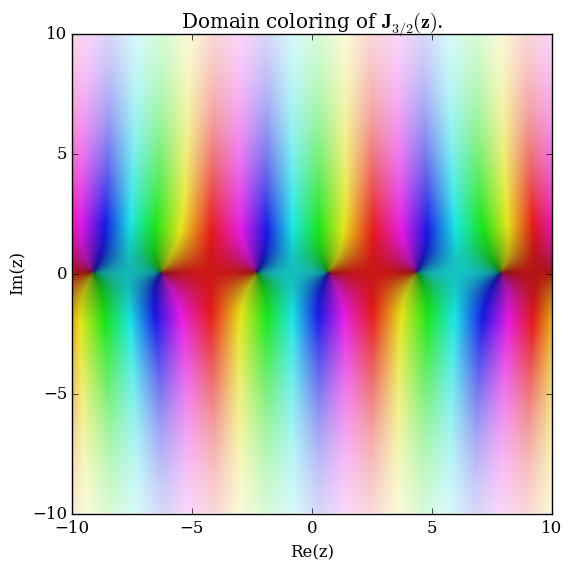
Domain coloring of $\mathbf{J}_{\frac{3}{2}}$.
Properties
Value of Anger at 0
Anger recurrence relation
Anger derivative recurrence
Relationship between Anger function and Bessel J sub nu
Relationship between Weber function and Anger function
Relationship between Anger function and Weber function
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next):12.3.1
