Difference between revisions of "Exponential integral Ei"
From specialfunctionswiki
| Line 19: | Line 19: | ||
[http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0018%7CLOG_0048 On certain definite integrals involving the exponential-integral - J.W.L. Glaisher] | [http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0018%7CLOG_0048 On certain definite integrals involving the exponential-integral - J.W.L. Glaisher] | ||
| − | + | {{:*-integral functions footer}} | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 23:09, 11 June 2016
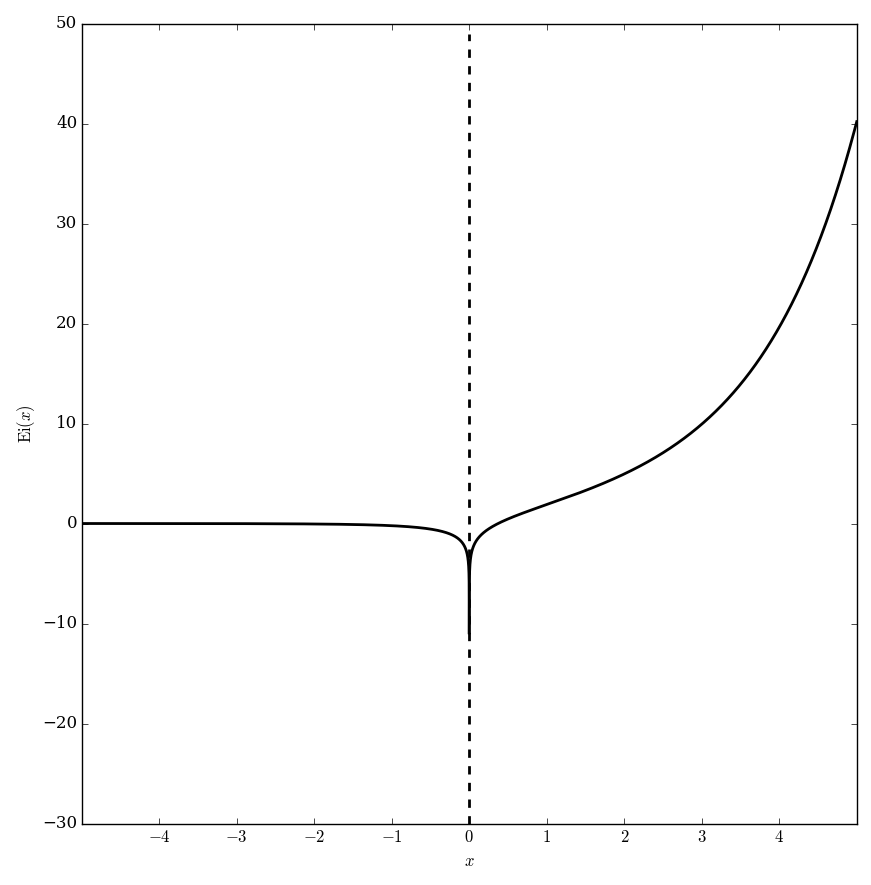
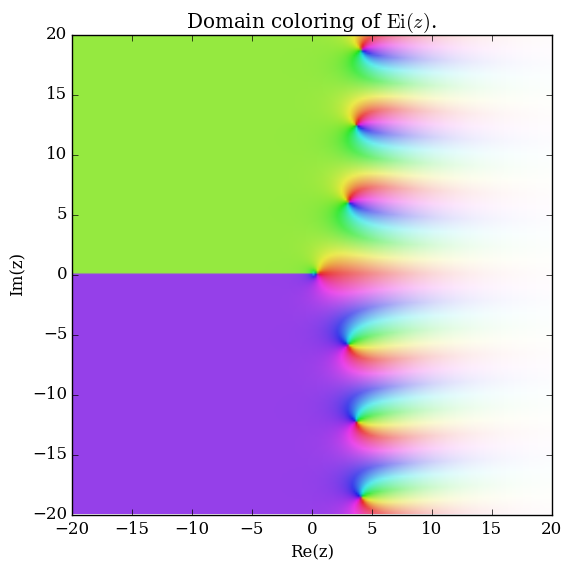
The exponential integral $\mathrm{Ei}$ is defined by $$\mathrm{Ei}(z) = \int_{-\infty}^x \dfrac{e^t}{t} \mathrm{d}t, \quad \left|\mathrm{arg}(-z) \right|<\pi.$$
Graph of $\mathrm{Ei}$.
Domain coloring of $\mathrm{Ei}$.
Properties
Relationship between logarithmic integral and exponential integral
Exponential integral Ei series
Relationship between exponential integral Ei, cosine integral, and sine integral
References
Exponential Integral and Related Functions
On certain definite integrals involving the exponential-integral - J.W.L. Glaisher
Exp integral $\mathrm{Ei}$
