Difference between revisions of "Bessel J"
(→Properties) |
|||
| Line 35: | Line 35: | ||
[http://www.johndcook.com/blog/2013/08/03/addition-formulas-for-bessel-functions/ Addition formulas for Bessel functions]<br /> | [http://www.johndcook.com/blog/2013/08/03/addition-formulas-for-bessel-functions/ Addition formulas for Bessel functions]<br /> | ||
[http://www.johndcook.com/Bessel_functions.html Relations between Bessel functions by John D. Cook] | [http://www.johndcook.com/Bessel_functions.html Relations between Bessel functions by John D. Cook] | ||
| + | |||
| + | =See Also= | ||
| + | [[Bessel Y]]<br /> | ||
<center>{{:Bessel functions footer}}</center> | <center>{{:Bessel functions footer}}</center> | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 20:36, 9 June 2016
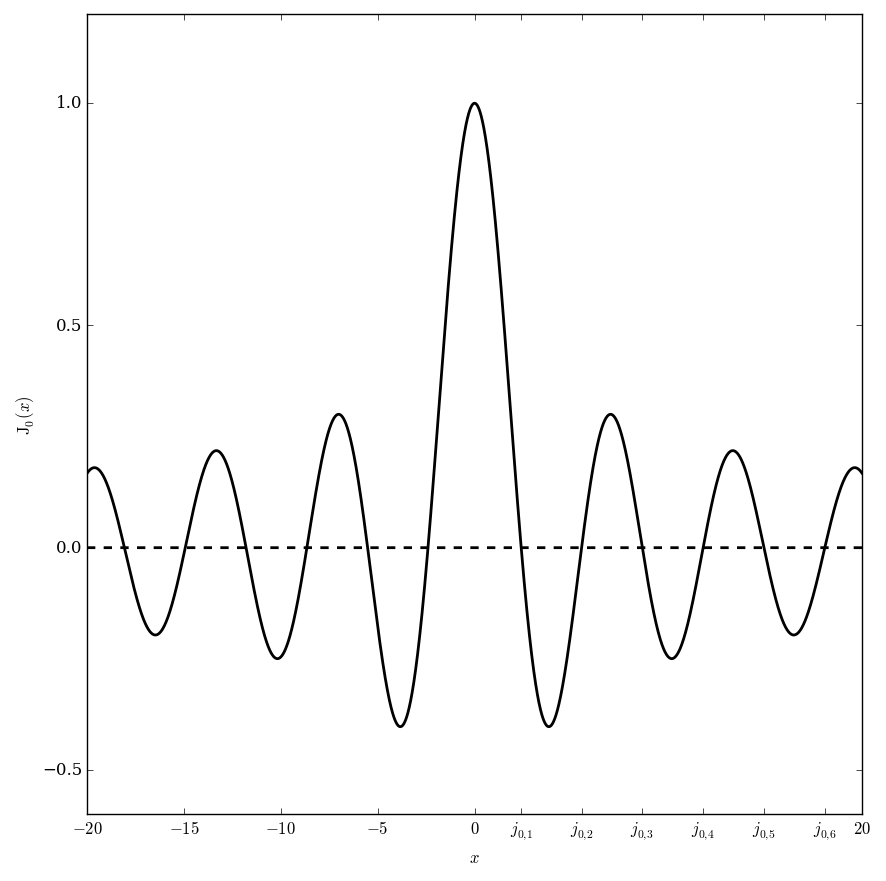
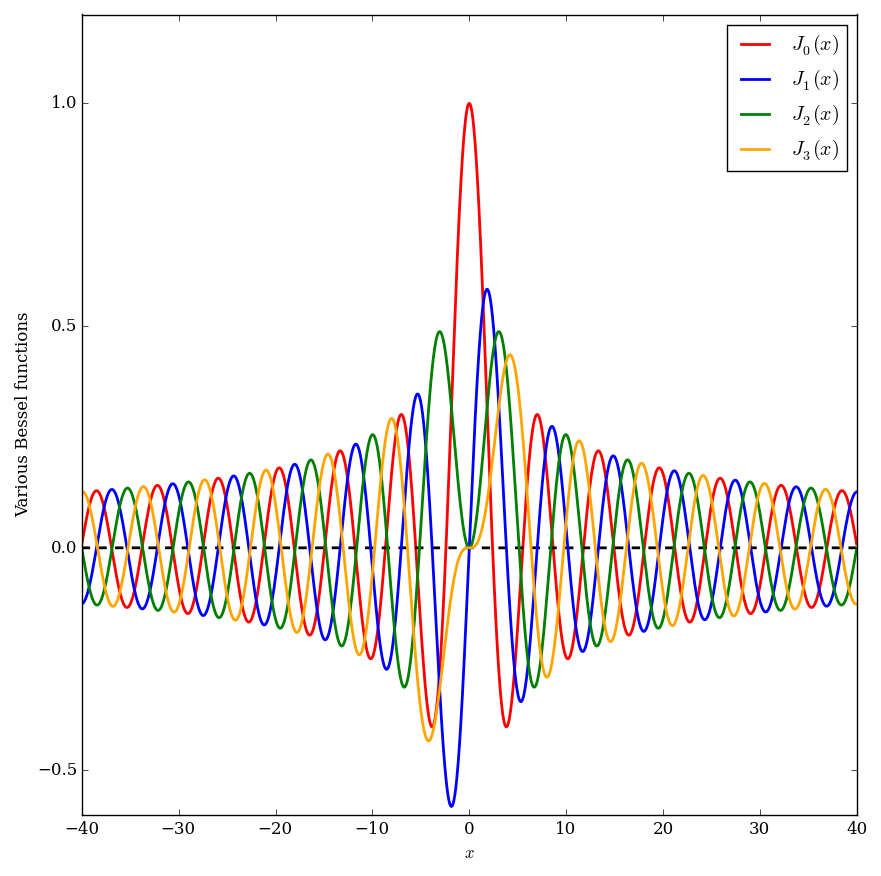
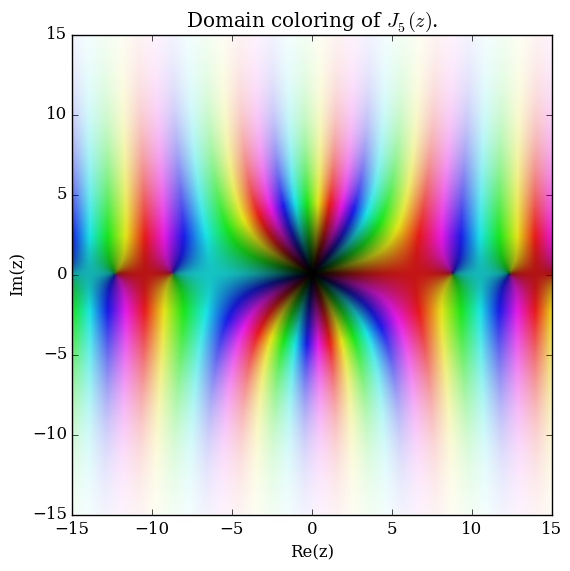
The Bessel functions of the first kind, $J_{\nu}$, have a power series expansion $$J_{\nu}(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{k! \Gamma(k+\nu+1)2^{2k+\nu}}z^{2k+\nu},$$ where $\Gamma$ denotes the gamma function.
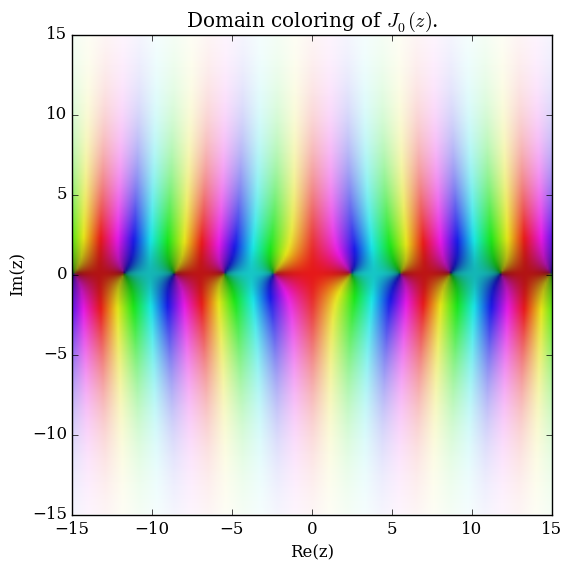
Domain coloring of $J_0$.
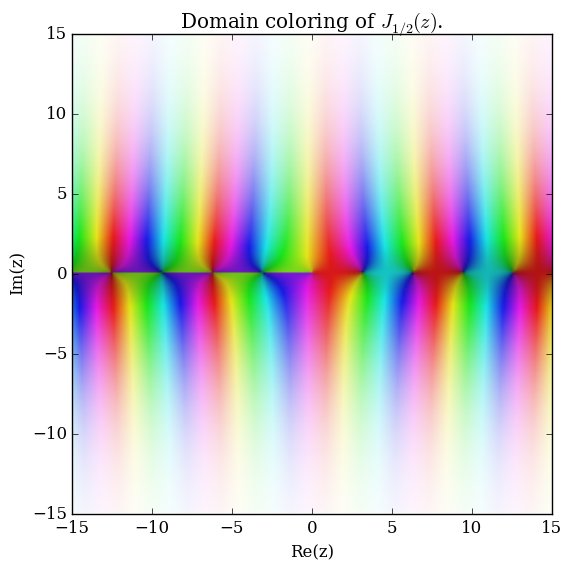
Domain coloring of $J_{\frac{1}{2}}$.
Domain coloring of $J_5$.
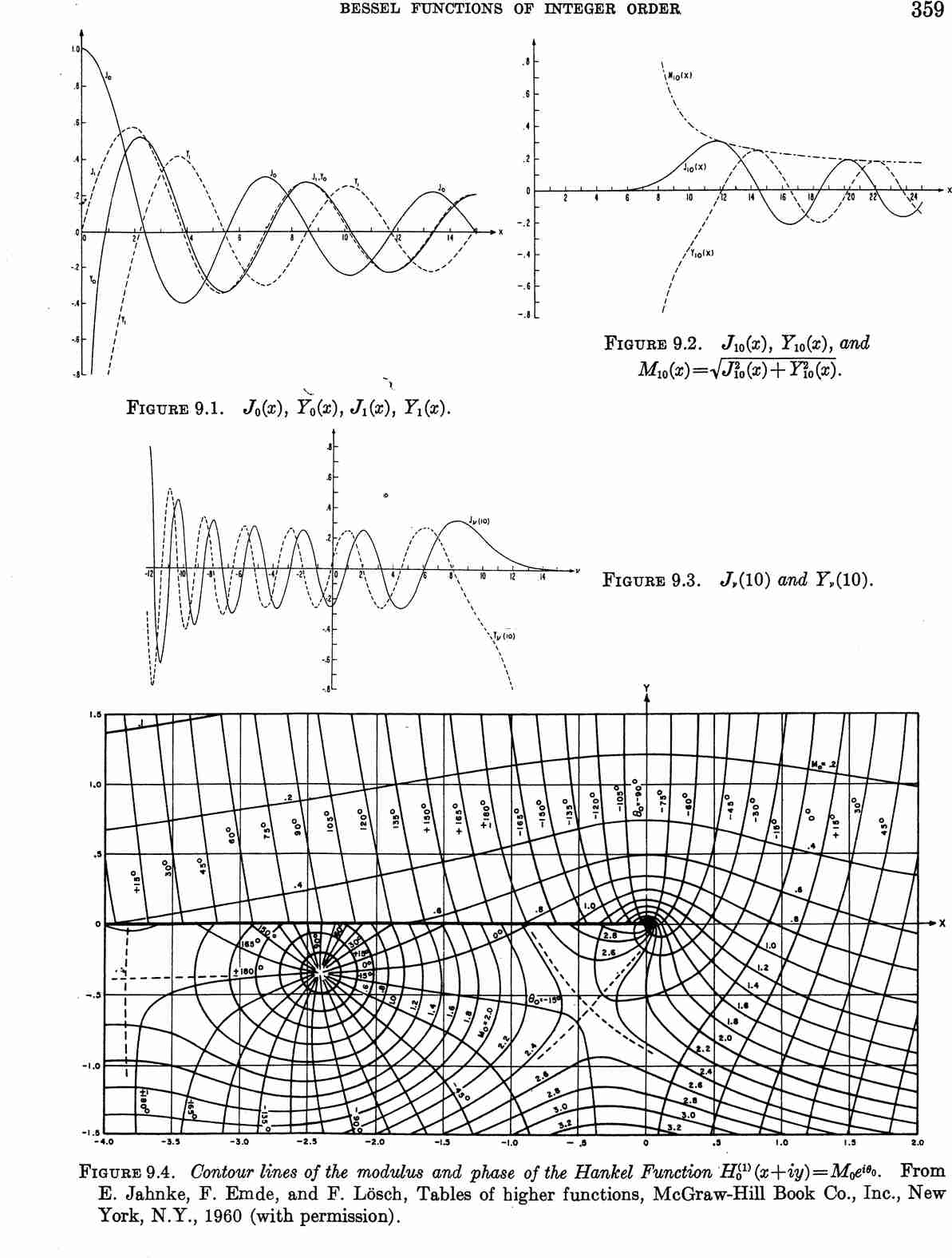
Bessel functions from Abramowitz&Stegun
Contents
Properties
Bessel polynomial in terms of Bessel functions
Bessel at n+1/2 in terms of Bessel polynomial
Bessel at -n-1/2 in terms of Bessel polynomial
Relationship between Bessel J and hypergeometric 0F1
Relationship between Bessel I and Bessel J
Relationship between Anger function and Bessel J
Videos
Bessel Equation and Bessel functions
Mod-1 Lec-6 Bessel Functions and Their Properties-I
Bessel's Equation by Free Academy
Taylor Series, Bessel, single Variable Calculus, Coursera.org
Ordinary Differential Equations Lecture 7—Bessel functions and the unit step function
Laplace transform of Bessel function order zero
Laplace transform: Integral over Bessel function is one
Orthogonal Properties of Bessel Function, Orthogonal Properties of Bessel Equation
Links
Addition formulas for Bessel functions
Relations between Bessel functions by John D. Cook