Revision as of 19:16, 10 June 2016

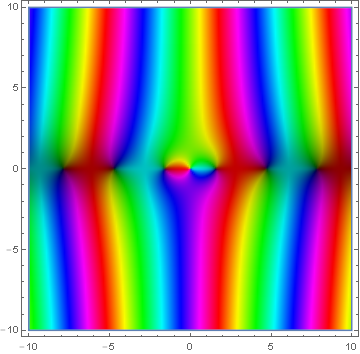
The spherical Bessel function of the second kind is $$y_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}} Y_{\nu+\frac{1}{2}}(z),$$ where $Y_{\nu}$ denotes the Bessel function of the second kind.

Properties

Theorem

The following formula holds for non-negative integers $n$: $$y_n(z)=(-1)^{n+1}z^n \left( \dfrac{1}{z} \dfrac{d}{dz} \right)^n \left( \dfrac{\cos z}{z} \right),$$ where $y_n$ denotes the spherical Bessel function of the second kind and $\cos$ denotes the cosine function.

Proof

References

References

Anger function

Bessel-Clifford

Bessel $J_{\nu}$

Bessel $Y_{\nu}$

Bessel $I_{\nu}$

Modified Bessel $K_{\nu}$

Spherical Bessel $j_{\nu}$

Spherical Bessel $y_{\nu}$