Difference between revisions of "Hankel H (1)"
From specialfunctionswiki
| Line 9: | Line 9: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| − | |||
| − | |||
=See Also= | =See Also= | ||
| Line 18: | Line 16: | ||
=References= | =References= | ||
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Bessel Y|next=Hankel H (1) in terms of csc and Bessel J}}: 9.1.3 | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Bessel Y|next=Hankel H (1) in terms of csc and Bessel J}}: 9.1.3 | ||
| + | |||
| + | {{:Hankel functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 04:02, 11 June 2016
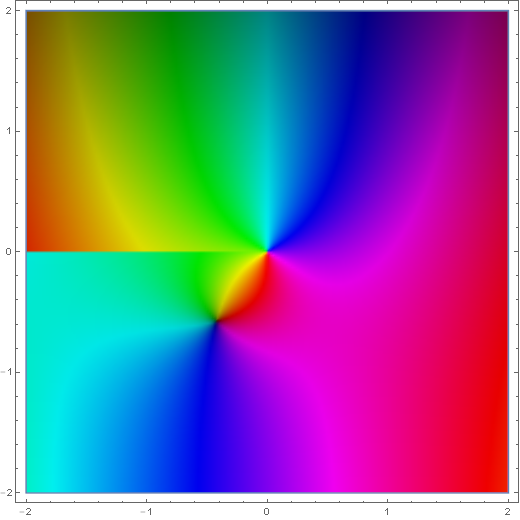
The Hankel functions of the first kind are defined by $$H_{\nu}^{(1)}(z)=J_{\nu}(z)+iY_{\nu}(z),$$ where $J_{\nu}$ is the Bessel function of the first kind and $Y_{\nu}$ is the Bessel function of the second kind. Note the similarity of these functions to the Hankel functions of the second kind.
Domain coloring of analytic continuation of $H_1^{(1)}(z)$.
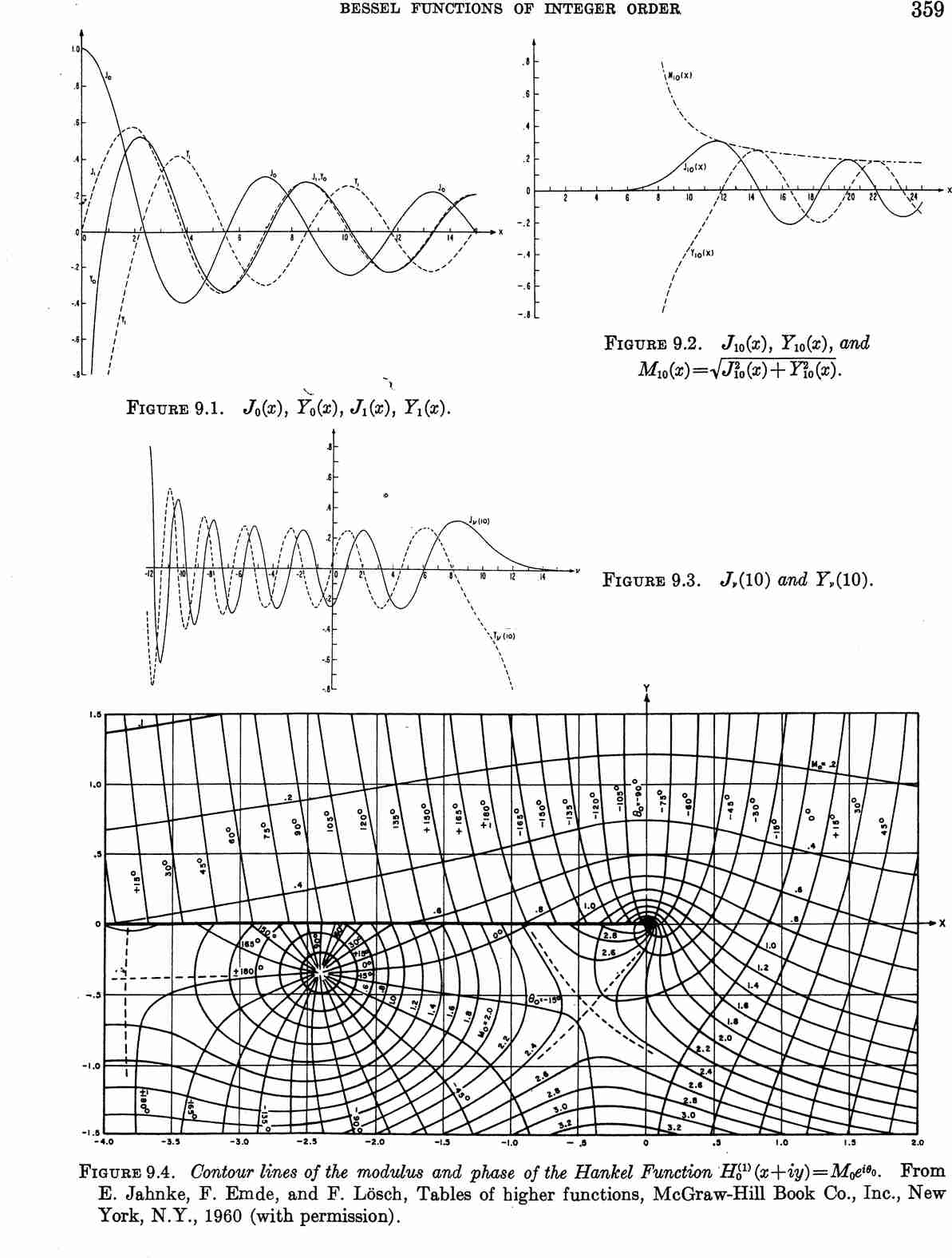
Bessel functions from Abramowitz&Stegun
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 9.1.3
Hankel $H_{\nu}^{(1)}$