|
|
| Line 10: |
Line 10: |
| | | | |
| | =Properties= | | =Properties= |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| + | [[Partial derivative of beta function]]<br /> |
| − | <strong>Theorem:</strong> $\psi(1)=-\gamma$ and for integers $n\geq 2$,
| |
| − | $$\psi(n)=-\gamma + \displaystyle\sum_{k=1}^{n-1} \dfrac{1}{k}$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> $\psi\left(\dfrac{1}{2}\right)=-\gamma-2\log(2)$ and for integers $n \geq 1$,
| |
| − | $$\psi \left( n + \dfrac{1}{2} \right) = -\gamma - 2 \log(2) + 2 \left( 1 + \dfrac{1}{3} + \ldots + \dfrac{1}{2n-1} \right).$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> $\psi(z+1) = \psi(z) + \dfrac{1}{z}$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> $\psi(z+n)=\dfrac{1}{(n-1)+z} + \dfrac{1}{(n-2)+z} + \ldots + \dfrac{1}{2+z} + \dfrac{1}{1+z} + \psi(1+z)$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> $\psi(1-z)=\psi(z) + \pi \cot(\pi z)$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> $\psi(2z)=\dfrac{1}{2}\psi(z) + \dfrac{1}{2} \psi \left( z + \dfrac{1}{2} \right) + \log(2)$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> $\psi(\overline{z})=\overline{\psi(z)}$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | {{:Partial derivative of beta function}}
| |
| | | | |
| | =See Also= | | =See Also= |
| Line 69: |
Line 18: |
| | | | |
| | =References= | | =References= |
| | + | * {{BookReference|Higher Transcendental Functions Volume I|1953|Harry Bateman|prev=findme|next=findme}}: $\S 1.7 (1)$ |
| | | | |
| | [[Category:SpecialFunction]] | | [[Category:SpecialFunction]] |
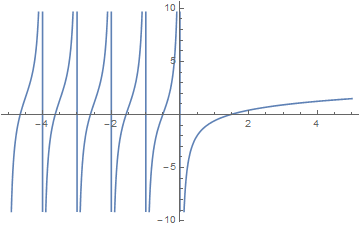
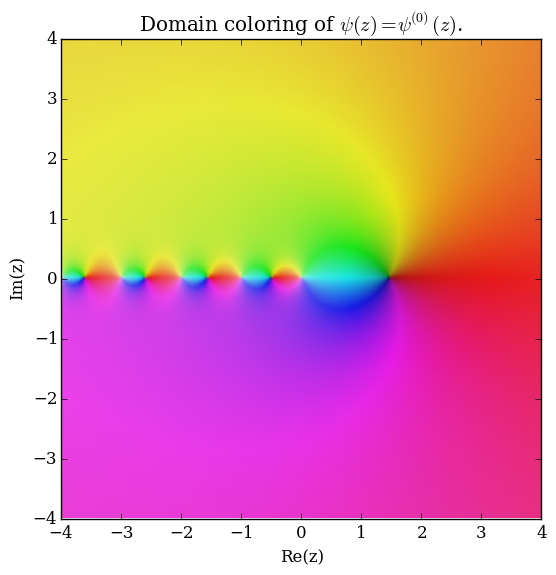
The digamma function $\psi$ is defined by
$$\psi(z) = \dfrac{\mathrm{d}}{\mathrm{d}z} \log \Gamma(z) = \dfrac{\Gamma'(z)}{\Gamma(z)}.$$