Difference between revisions of "Prime zeta P"
From specialfunctionswiki
(→External links) |
|||
| Line 15: | Line 15: | ||
=External links= | =External links= | ||
| − | [http://math.stackexchange.com/questions/49383/how-does-sum-px-p-s-grow-asymptotically-for-textres-1/ | + | [http://math.stackexchange.com/questions/49383/how-does-sum-px-p-s-grow-asymptotically-for-textres-1/ How does ∑p<xp−s grow asymptotically for Re(s)<1?] <br /> |
=References= | =References= | ||
Revision as of 19:33, 15 June 2016
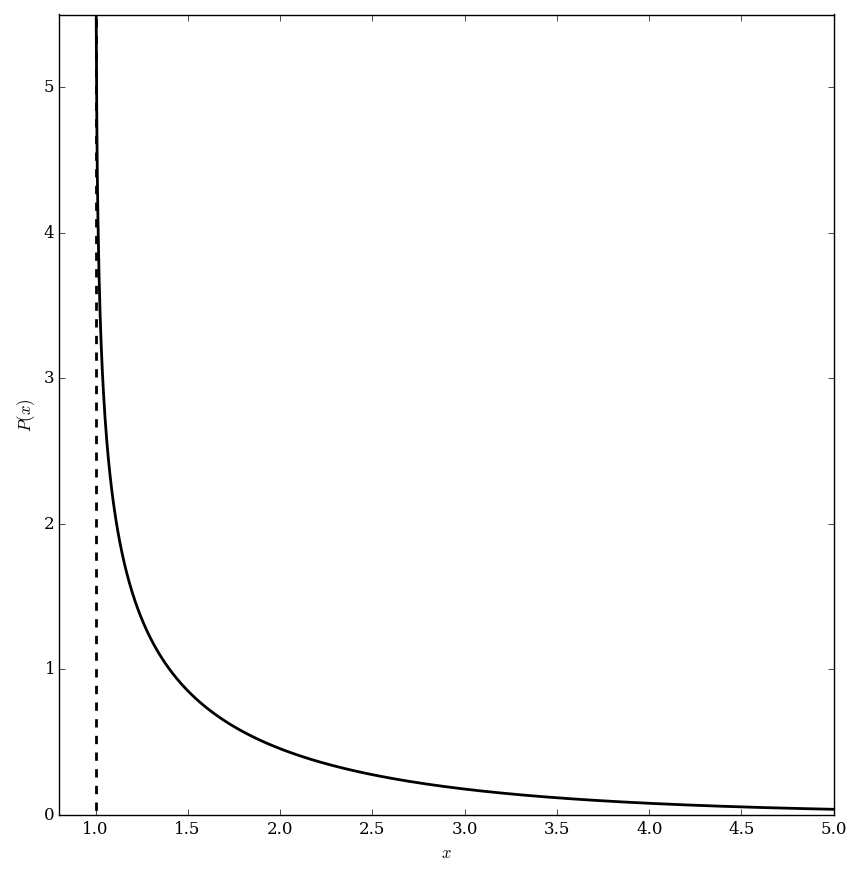
The prime zeta function is defined by $$P(z) = \displaystyle\sum_{p \mathrm{\hspace{2pt} prime}} \dfrac{1}{p^z},$$ where $\mathrm{Re}(z)>1$. It can be extended outside of this domain via analytic continuation.
Properties
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
External links
How does ∑p<xp−s grow asymptotically for Re(s)<1?