Difference between revisions of "Mangoldt"
From specialfunctionswiki
| Line 5: | Line 5: | ||
0 &; \mathrm{otherwise}. | 0 &; \mathrm{otherwise}. | ||
\end{array} \right.$$ | \end{array} \right.$$ | ||
| + | |||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
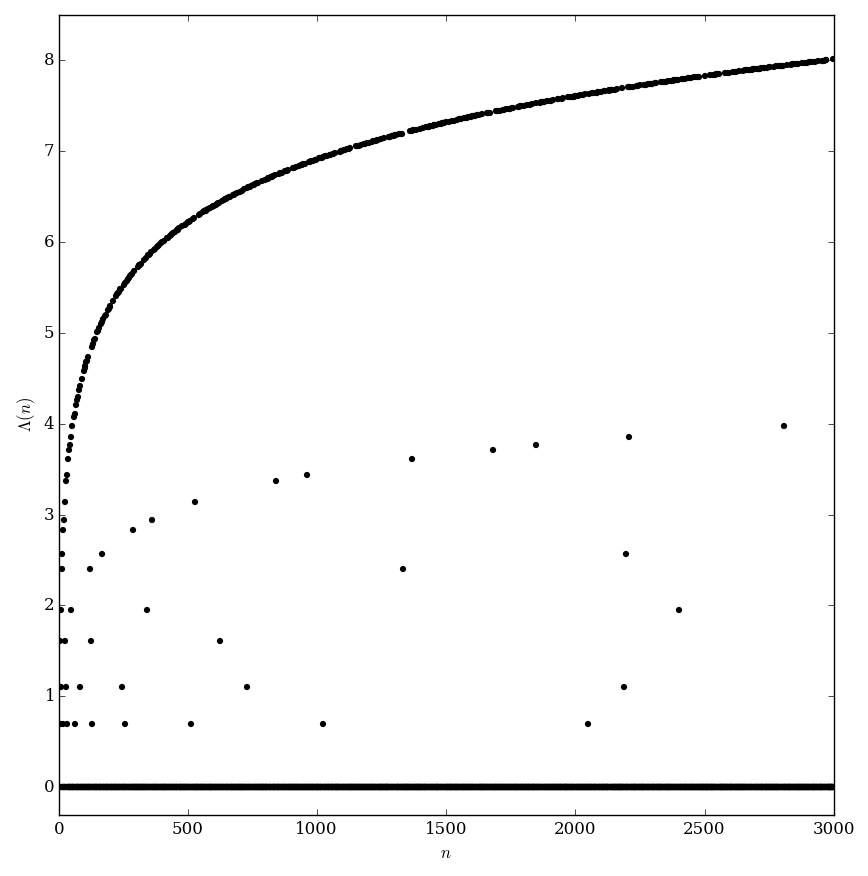
| + | File:Mangoldtplot.png|Graph of $\Lambda$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
Revision as of 05:58, 22 June 2016
The Mangoldt function is defined by the formula $$\Lambda(n) = \left\{ \begin{array}{ll} \log p &; n=p^k \mathrm{\hspace{2pt}for\hspace{2pt}some\hspace{2pt}prime\hspace{2pt}}p\mathrm{\hspace{2pt}and\hspace{2pt}integer\hspace{2pt}}k\geq 1, \\ 0 &; \mathrm{otherwise}. \end{array} \right.$$
Graph of $\Lambda$.
Properties
Relationship between logarithm and Mangoldt
Videos
Number Theory 31: Liouville and mangoldt functions
Number theory: Arithmetic functions #1
