Difference between revisions of "Gamma"
(→References) |
|||
| Line 39: | Line 39: | ||
[https://www.youtube.com/watch?v=XAoe4th0F1k Gamma function at 1/2]<br /> | [https://www.youtube.com/watch?v=XAoe4th0F1k Gamma function at 1/2]<br /> | ||
[https://www.youtube.com/watch?v=l7LoSBv6o2k Contour Integral Definition of the Gamma Function ]<br /> | [https://www.youtube.com/watch?v=l7LoSBv6o2k Contour Integral Definition of the Gamma Function ]<br /> | ||
| + | |||
| + | =External links= | ||
| + | [http://ocw.mit.edu/courses/mathematics/18-104-seminar-in-analysis-applications-to-number-theory-fall-2006/projects/chan.pdf The sine product formula and the gamma function]<br /> | ||
| + | [http://www.jstor.org/discover/10.2307/2309786?sid=21105065140641&uid=3739256&uid=2129&uid=70&uid=3739744&uid=4&uid=2 Leonhard Euler's Integral: A Historical Profile of the Gamma Function]<br /> | ||
=See Also= | =See Also= | ||
| Line 50: | Line 54: | ||
* {{BookReference|Higher Transcendental Functions Volume I|1953|Harry Bateman|next=Gamma(z) as integral of a power of log(1/t) for Re(z) greater than 0}}: $\S 1.1 (1)$ | * {{BookReference|Higher Transcendental Functions Volume I|1953|Harry Bateman|next=Gamma(z) as integral of a power of log(1/t) for Re(z) greater than 0}}: $\S 1.1 (1)$ | ||
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Gauss' formula for gamma function}}: $6.1.1$ | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Gauss' formula for gamma function}}: $6.1.1$ | ||
| − | |||
| − | |||
| − | |||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 16:19, 21 June 2016
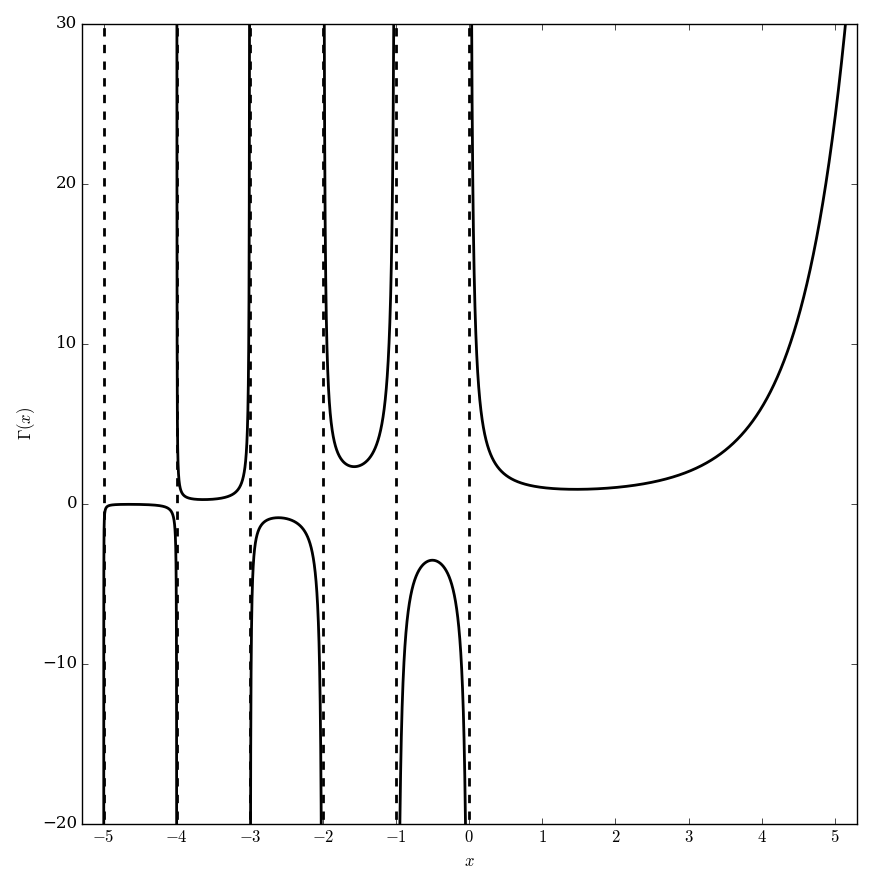
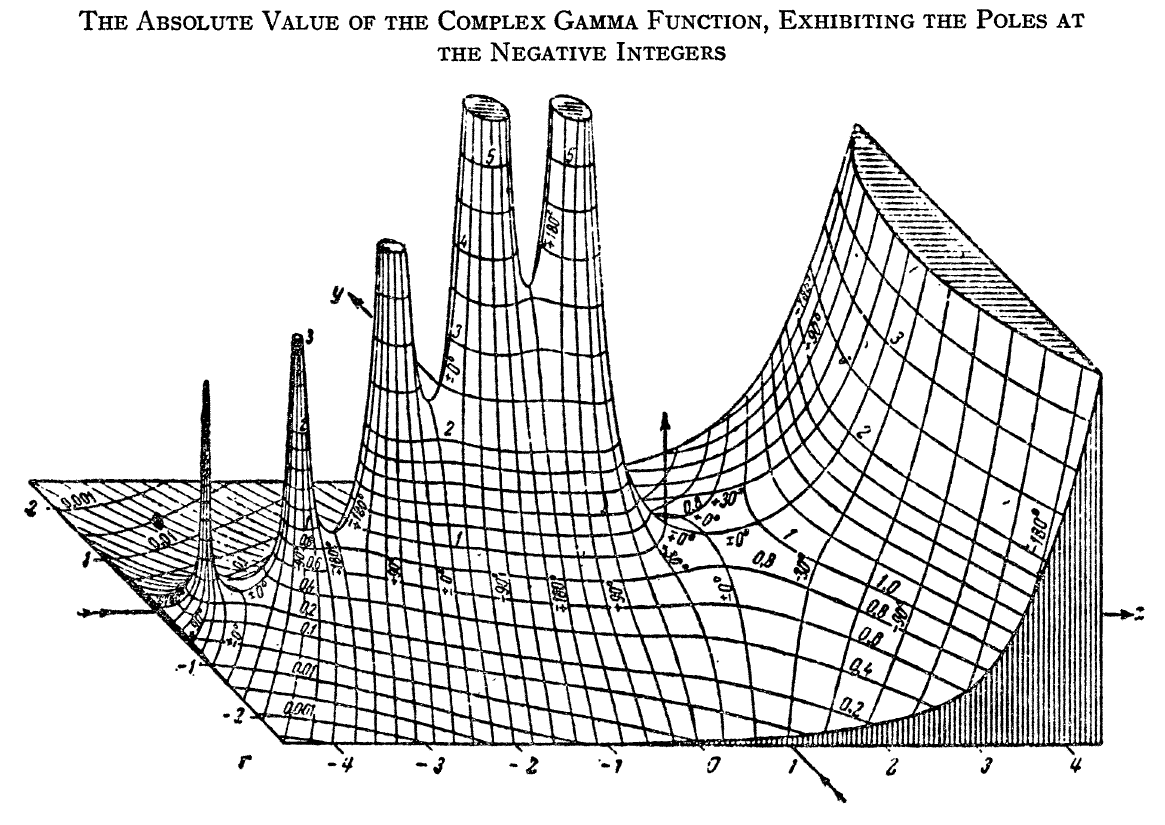
The gamma function $\Gamma \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$ is the function initially defined for $x>0$ by the integral by the formula $$\Gamma(x)=\displaystyle\int_0^{\infty} \xi^{x-1}e^{-\xi} \mathrm{d}\xi.$$ The analytic continuation of $\Gamma$ leads to a meromorphic function with poles at the negative integers.
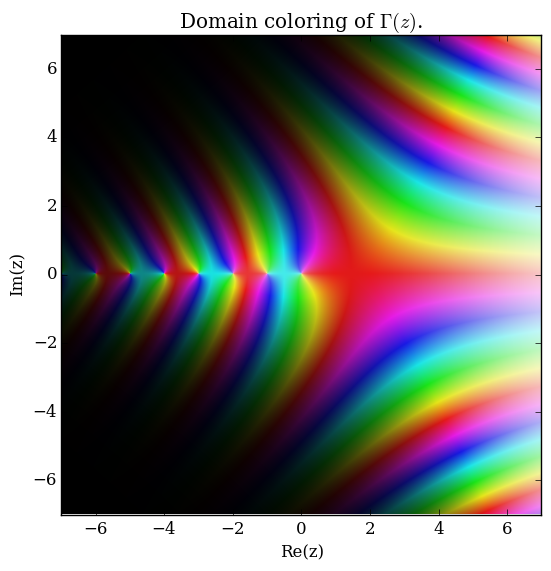
Domain coloring of $\Gamma$.
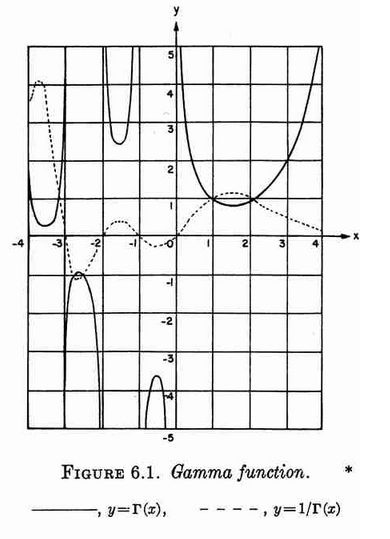
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
Properties
Gamma(z) as integral of a power of log(1/t) for Re(z) greater than 0
Gamma function written as a limit of a factorial, exponential, and a rising factorial
Gamma function written as infinite product
Value of Gamma(1)
Factorial property of gamma
Gamma at positive integers
Relationship between Hurwitz zeta and gamma function
Gamma-Sine Relation
Bohr-Mollerup theorem
Videos
Gamma Function (playlist)
The Gamma Function: intro (5)
Gamma Integral Function - Introduction
Gamma function
Mod-04 Lec-09 Analytic continuation and the gamma function (Part I)
gamma function - Part 1
Beta Function, Gamma Function and their Properties
What's the Gamma Function?
euler gamma function
Thermodynamics 19 a : Gamma Function 1/2
The Gamma Function: why 0!=1 (5)
Gamma Function Of One-Half: Part 1
Gamma Function Of One-Half: Part 2
Gamma function at 1/2
Contour Integral Definition of the Gamma Function
External links
The sine product formula and the gamma function
Leonhard Euler's Integral: A Historical Profile of the Gamma Function
See Also
Loggamma
Polygamma
Reciprocal gamma
References
- 1895: Johann Heinrich Graf: Einleitung in die Theorie der Gammafunktion und der Euler'schen Integrale ... (previous) ... (next): $\S 3 (15_a)$
- 1920: Edmund Taylor Whittaker and George Neville Watson: A course of modern analysis ... (previous) ... (next): $\S 12 \cdot 1$
- 1953: Harry Bateman: Higher Transcendental Functions Volume I ... (next): $\S 1.1 (1)$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $6.1.1$