Difference between revisions of "Digamma"
From specialfunctionswiki
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
[[Partial derivative of beta function]]<br /> | [[Partial derivative of beta function]]<br /> | ||
| + | [[Digamma functional equation]]<br /> | ||
| + | [[Digamma at n+1]]<br /> | ||
=See Also= | =See Also= | ||
Revision as of 15:45, 23 June 2016
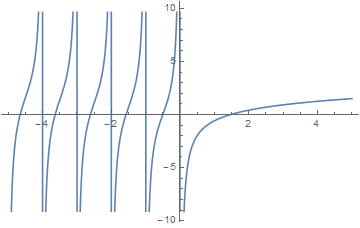
The digamma function $\psi$ is defined by $$\psi(z) = \dfrac{\mathrm{d}}{\mathrm{d}z} \log \Gamma(z) = \dfrac{\Gamma'(z)}{\Gamma(z)}.$$
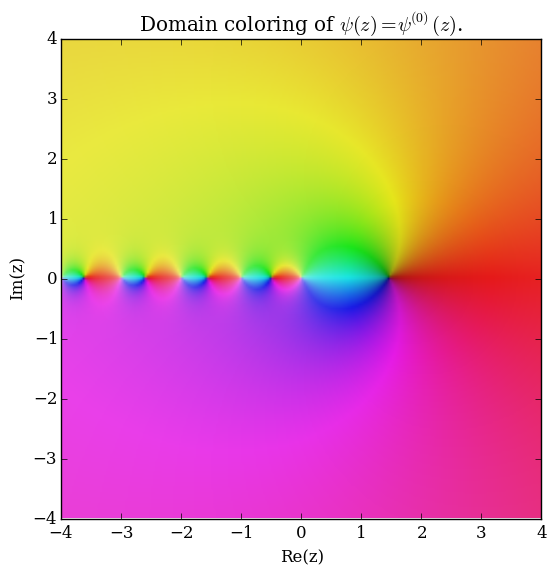
Domain coloring of $\psi(z)$.
Properties
Partial derivative of beta function
Digamma functional equation
Digamma at n+1
See Also
Gamma function
Polygamma function
Trigamma function
References
- 1953: Harry Bateman: Higher Transcendental Functions Volume I ... (previous) ... (next): $\S 1.7 (1)$