Difference between revisions of "Arcsinh"
From specialfunctionswiki
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
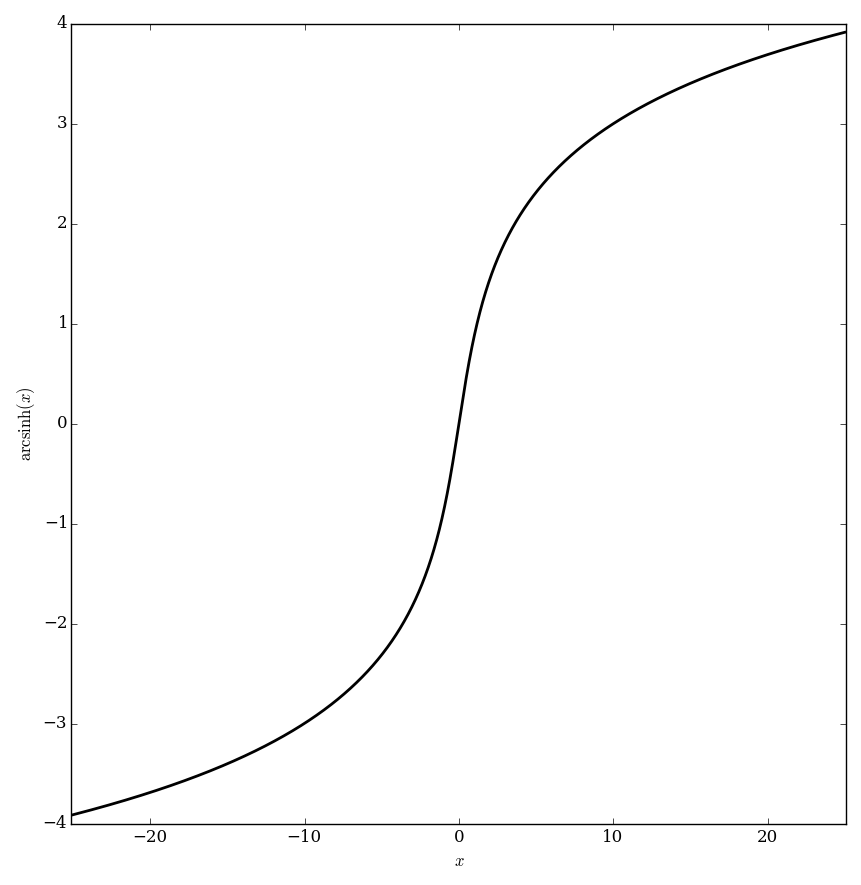
| − | The inverse hyperbolic sine function $\mathrm{arcsinh | + | The inverse hyperbolic sine function $\mathrm{arcsinh}$ is function is the [[inverse function]] of the [[sinh|hyperbolic sine]] function. It may be defined by |
| + | $$\mathrm{arcsinh}(z)=\log \left(z + \sqrt{1+z^2} \right).$$ | ||
<div align="center"> | <div align="center"> | ||
Revision as of 23:49, 15 September 2016
The inverse hyperbolic sine function $\mathrm{arcsinh}$ is function is the inverse function of the hyperbolic sine function. It may be defined by $$\mathrm{arcsinh}(z)=\log \left(z + \sqrt{1+z^2} \right).$$
Plot of $\mathrm{arcsinh}$ on $[-10,10]$.
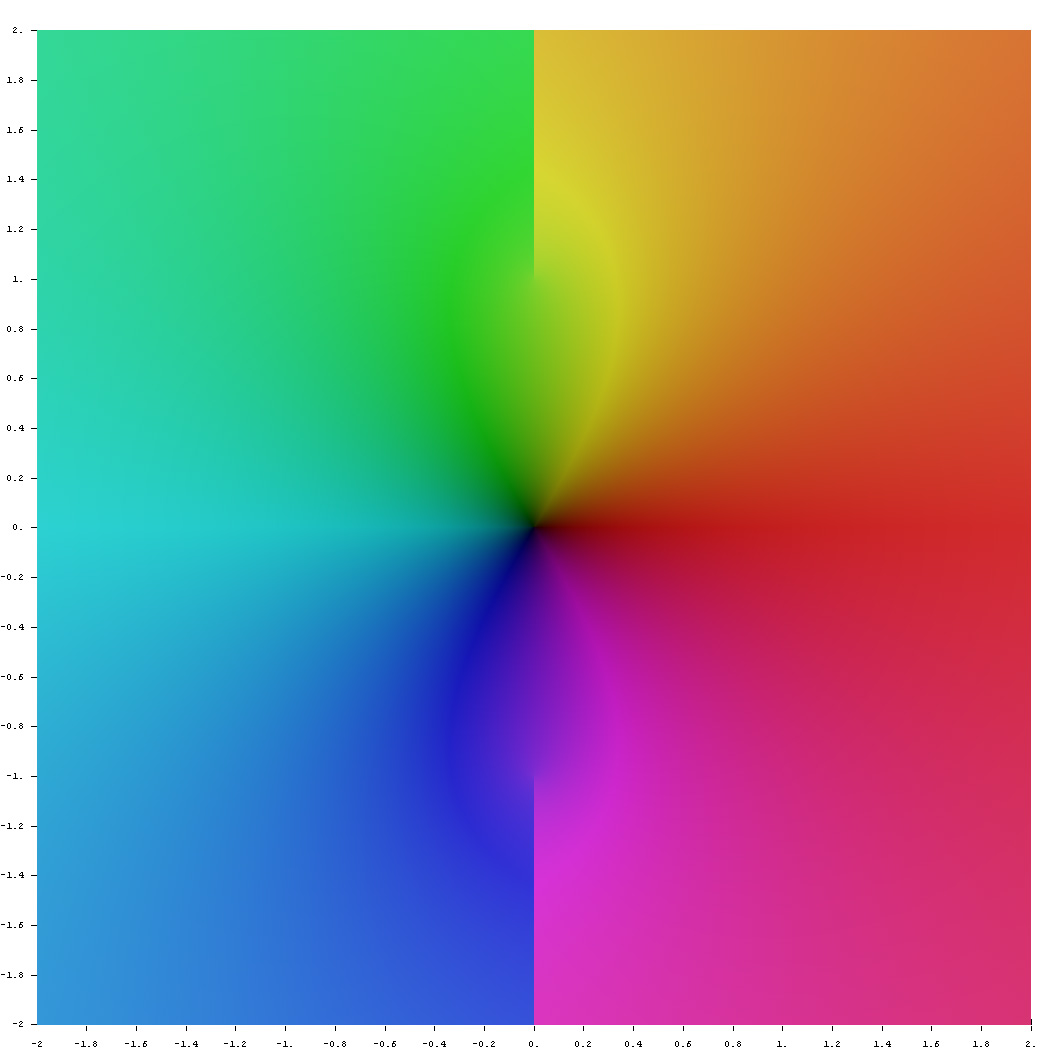
Domain coloring of analytic continuation of $\mathrm{arcsinh}$.
