Difference between revisions of "Exponential integral Ei"
From specialfunctionswiki
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
| + | [[Exponential integral with negative exponent on e in definition]]<br /> | ||
[[Relationship between logarithmic integral and exponential integral]]<br /> | [[Relationship between logarithmic integral and exponential integral]]<br /> | ||
[[Exponential integral Ei series]]<br /> | [[Exponential integral Ei series]]<br /> | ||
Revision as of 00:38, 25 June 2017
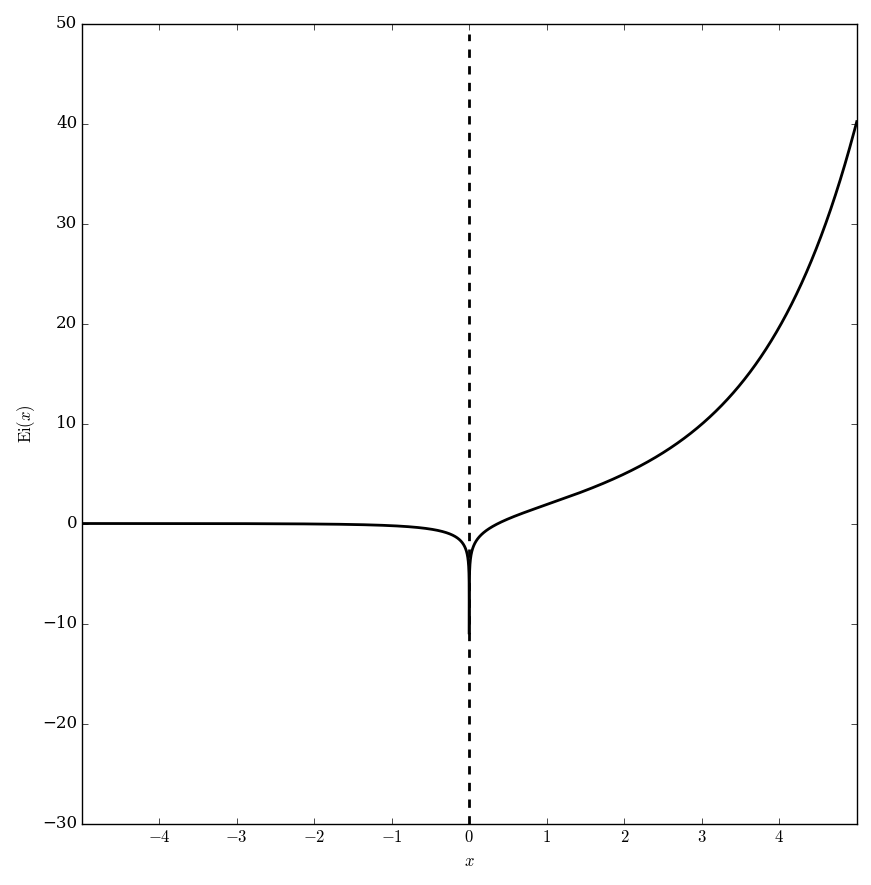
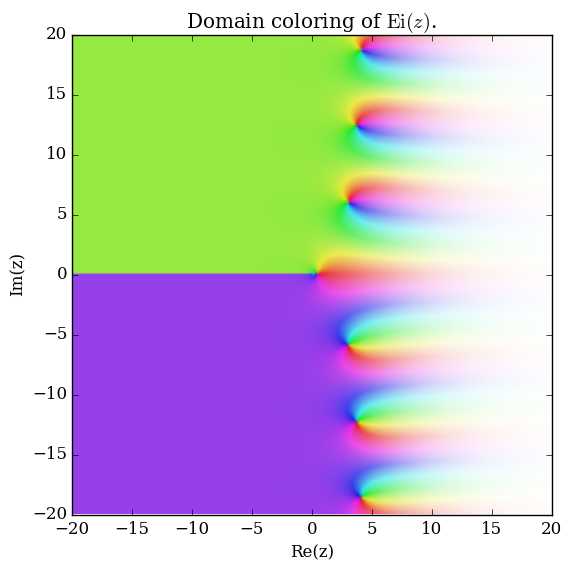
The exponential integral $\mathrm{Ei}$ is defined for $x>0$ by $$\mathrm{Ei}(x) = \int_{-\infty}^x \dfrac{e^t}{t} \mathrm{d}t.$$
Properties
Exponential integral with negative exponent on e in definition
Relationship between logarithmic integral and exponential integral
Exponential integral Ei series
Relationship between exponential integral Ei, cosine integral, and sine integral
See Also
References
- James Whitbread Lee Glaisher: On certain definite integrals involving the exponential-integral (1881)... (next)
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $5.1.2$