Difference between revisions of "Exponential integral E"
From specialfunctionswiki
(→Videos) |
|||
| Line 21: | Line 21: | ||
=Videos= | =Videos= | ||
| − | [https://www.youtube.com/watch?v=TppV_yDY3EQ Laplace transform of exponential integral]<br /> | + | [https://www.youtube.com/watch?v=TppV_yDY3EQ Laplace transform of exponential integral (2 January 2015)]<br /> |
=See Also= | =See Also= | ||
Revision as of 23:58, 10 December 2016
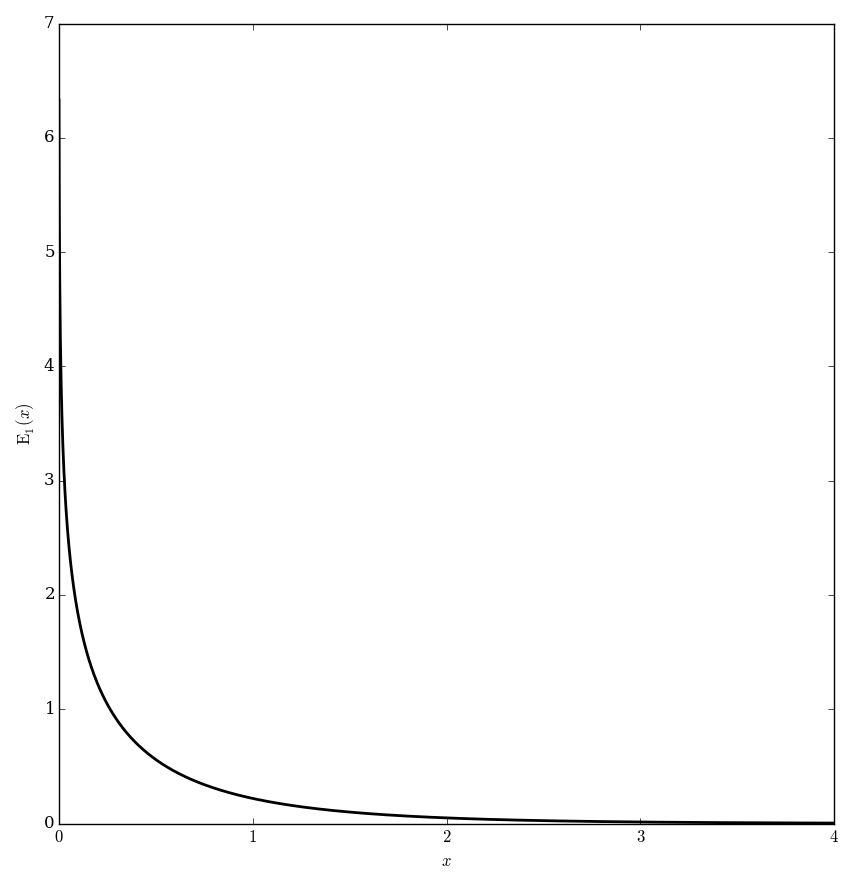
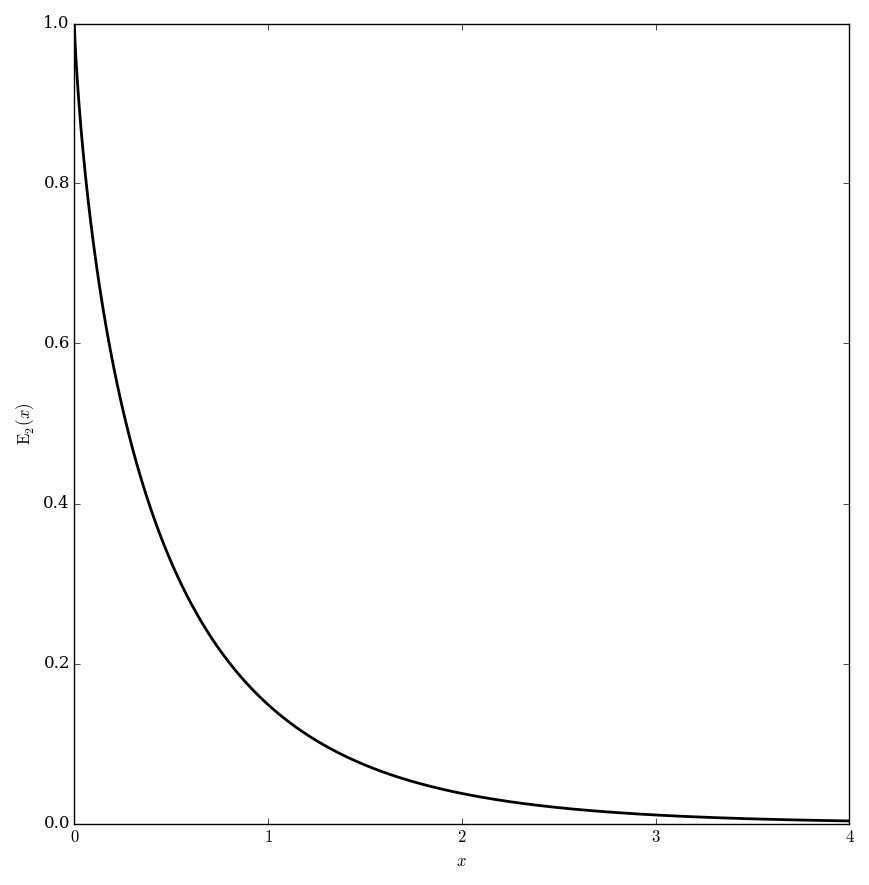
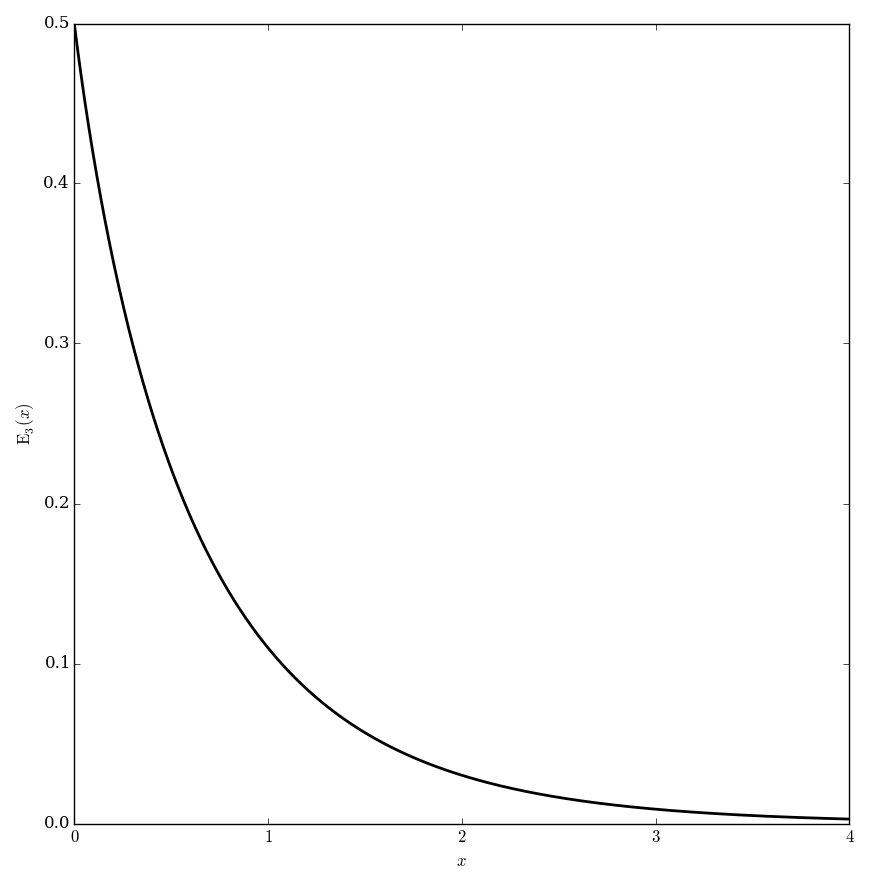
The exponential integral functions $E_n$ are defined for $\left|\mathrm{arg \hspace{2pt}}z\right|<\pi$ by $$E_1(z) = \displaystyle\int_1^{\infty} \dfrac{e^{-t}}{t} \mathrm{d}t,$$ and $$E_n(z)=\displaystyle\int_1^{\infty} \dfrac{e^{-zt}}{t^n} \mathrm{d}t.$$
Graph of $\mathrm{E}_1$.
Graph of $\mathrm{E}_2$.
Graph of $\mathrm{E}_3$.
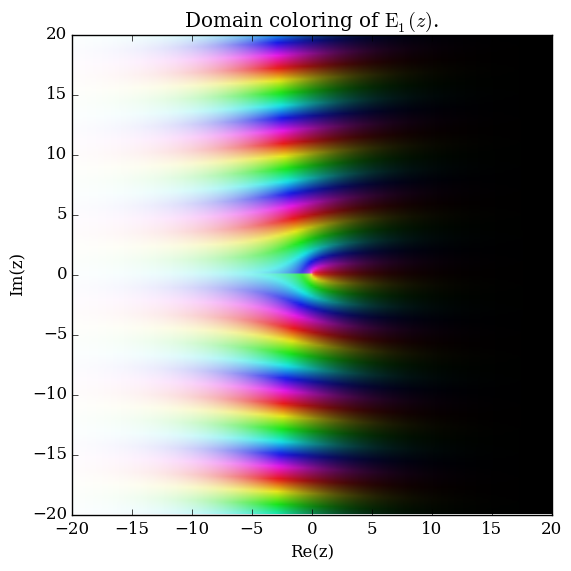
Domain coloring of $\mathrm{E}_1$.
Domain coloring of $\mathrm{E}_2$.
Properties
Relationship between the exponential integral and upper incomplete gamma function
Symmetry relation of exponential integral E
Recurrence relation of exponential integral E
Videos
Laplace transform of exponential integral (2 January 2015)
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $5.1.1$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $5.1.4$
