Difference between revisions of "Sine integral"
From specialfunctionswiki
(→Properties) |
|||
| Line 12: | Line 12: | ||
=Properties= | =Properties= | ||
| + | [[Derivative of sine integral]]<br /> | ||
| + | [[Antiderivative of sine integral]]<br /> | ||
[[Relationship between exponential integral Ei, cosine integral, and sine integral]]<br /> | [[Relationship between exponential integral Ei, cosine integral, and sine integral]]<br /> | ||
Revision as of 19:44, 10 December 2016
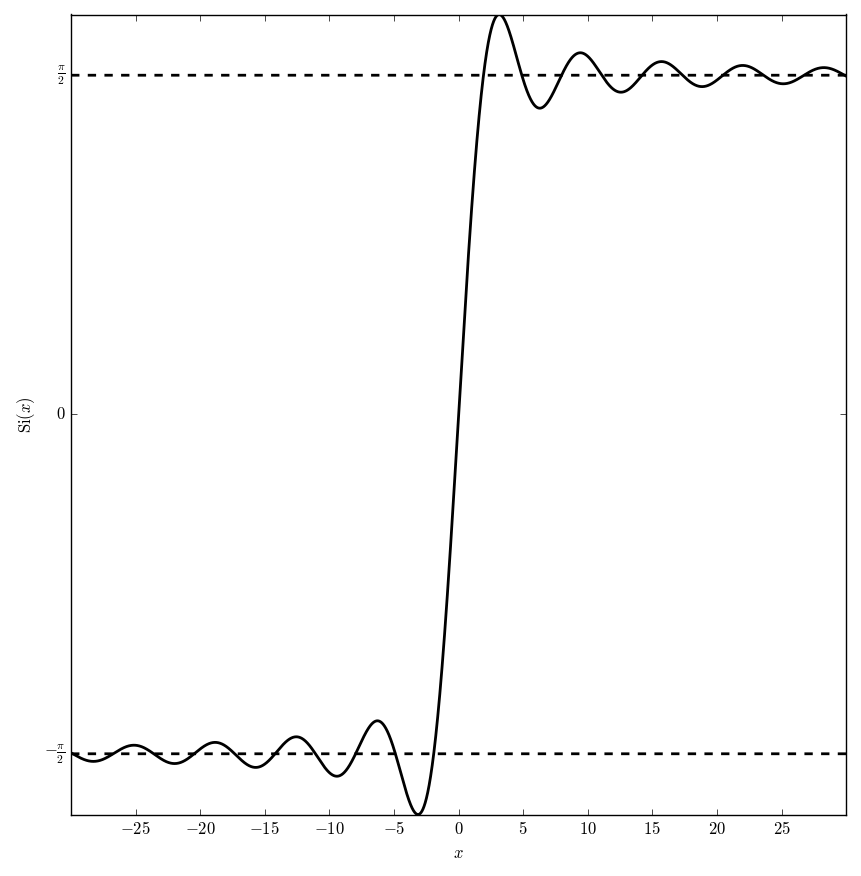
The sine integral is defined by $$\mathrm{Si}(z) = \displaystyle\int_0^z \mathrm{sinc}(t) \mathrm{d}t, \quad |\mathrm{arg} z|<\pi,$$ where $\mathrm{sinc}$ denotes the sinc function.
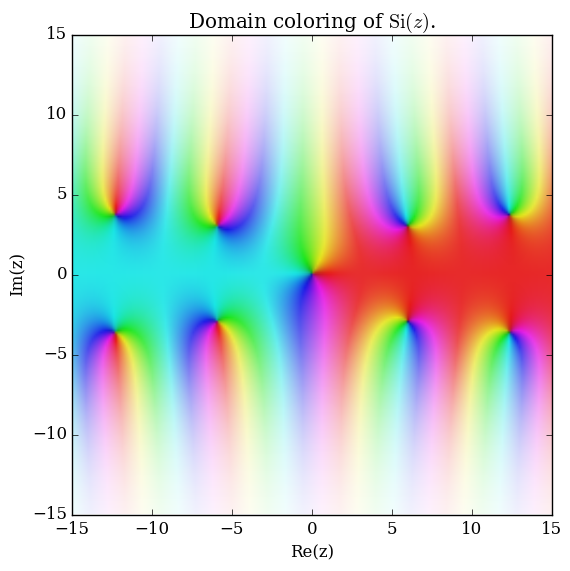
Domain coloring of $\mathrm{Si}$.
Properties
Derivative of sine integral
Antiderivative of sine integral
Relationship between exponential integral Ei, cosine integral, and sine integral
Videos
Laplace Transform of Sine Integral
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous): $5.2.1$