Difference between revisions of "Arctanh"
From specialfunctionswiki
(→Properties) |
|||
| Line 12: | Line 12: | ||
=Properties= | =Properties= | ||
[[Derivative of arctanh]] <br /> | [[Derivative of arctanh]] <br /> | ||
| + | [[Antiderivative of arctanh]]<br /> | ||
[[Derivative of Legendre chi]] <br /> | [[Derivative of Legendre chi]] <br /> | ||
Latest revision as of 23:47, 11 December 2016
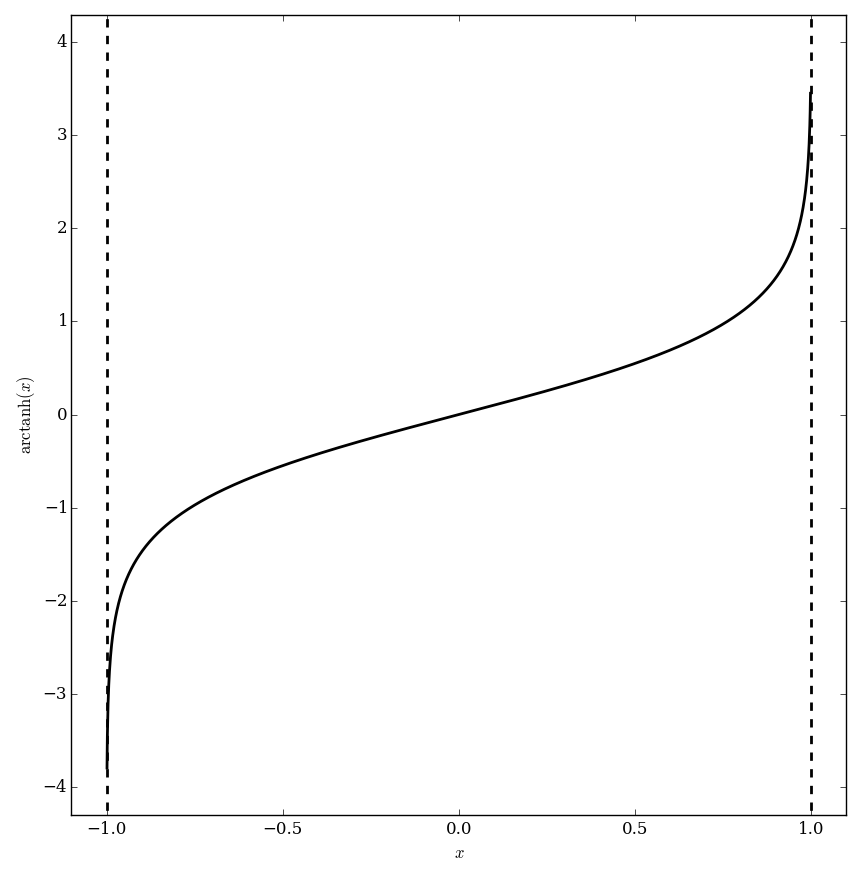
The inverse hyperbolic tangent function $\mathrm{arctanh}$ is the inverse function of the hyperbolic tangent function. It may be defined by $$\mathrm{arctanh}(z) = \dfrac{\log(1+z)}{2} - \dfrac{\log(1-z)}{2},$$ where $\log$ denotes the logarithm.
Plot of $\mathrm{arctanh}$ on $(-1,1)$.
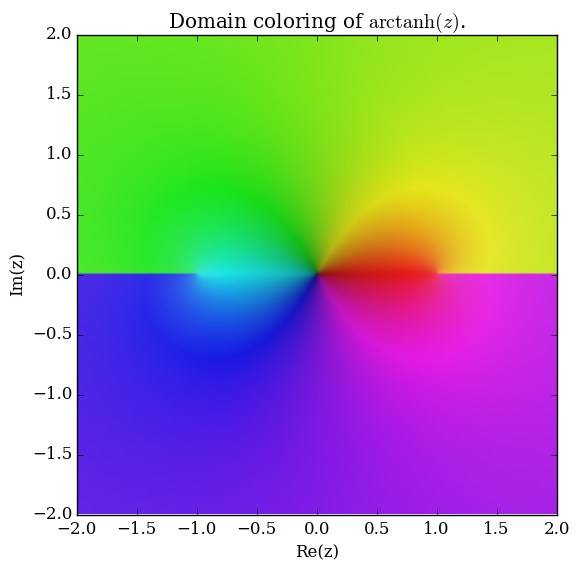
Domain coloring of $\mathrm{arctanh}$.
Properties
Derivative of arctanh
Antiderivative of arctanh
Derivative of Legendre chi
