Difference between revisions of "Airy Bi"
From specialfunctionswiki
(→Videos) |
|||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | + | ||
The Airy function $\mathrm{Bi}$ (sometimes called the "Bairy function") is a solution of the [[Airy differential equation]] | The Airy function $\mathrm{Bi}$ (sometimes called the "Bairy function") is a solution of the [[Airy differential equation]] | ||
| − | $$y''(z)-zy(z)=0,$$ | + | $$y' '(z)-zy(z)=0,$$ |
| − | which is linearly independent from the [[Airy Ai]] function. | + | which is [[linearly independent]] from the [[Airy Ai]] function. |
<div align="center"> | <div align="center"> | ||
| Line 32: | Line 32: | ||
[[Scorer Gi]] <br /> | [[Scorer Gi]] <br /> | ||
[[Scorer Hi]] <br /> | [[Scorer Hi]] <br /> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 16:07, 21 October 2017
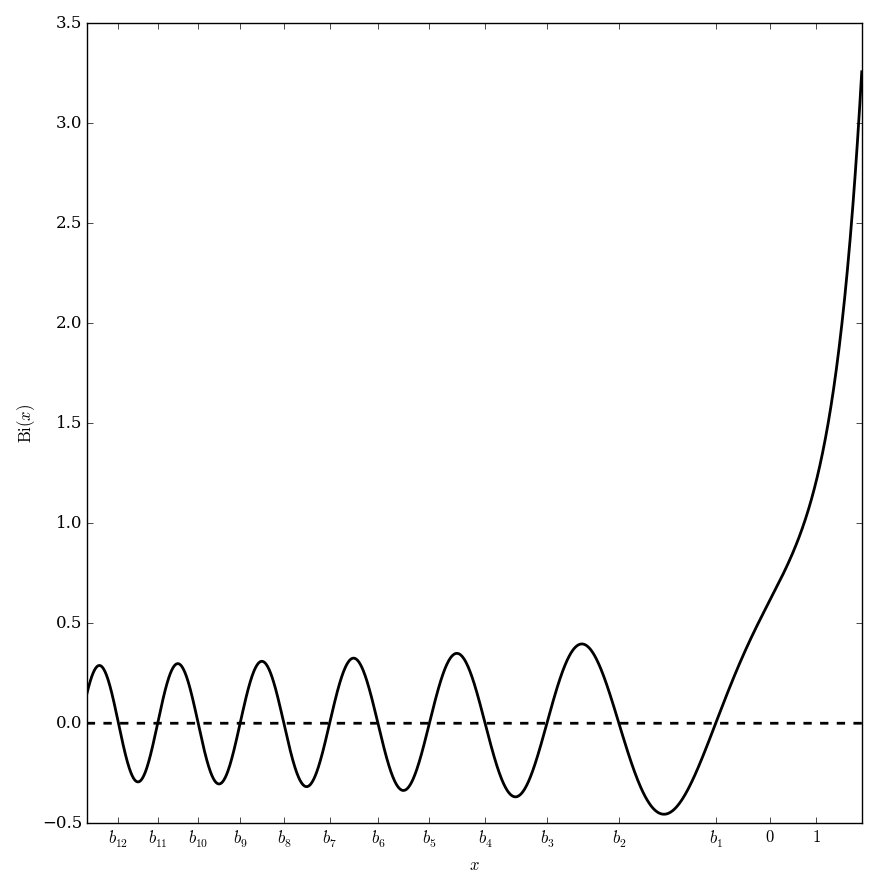
The Airy function $\mathrm{Bi}$ (sometimes called the "Bairy function") is a solution of the Airy differential equation
$$y' '(z)-zy(z)=0,$$
which is linearly independent from the Airy Ai function.
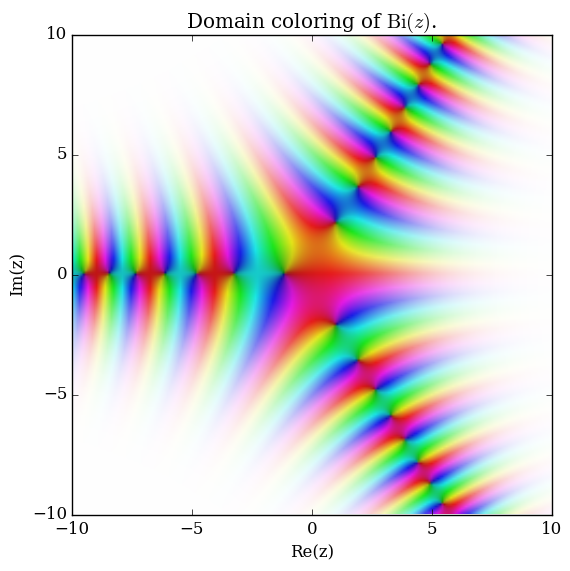
Domain coloring of $\mathrm{Bi}$.
Properties
Relationship between Airy Bi and modified Bessel I
Relationship between Scorer Gi and Airy functions
Relationship between Scorer Hi and Airy functions
Videos
Leading Tsunami wave reaching the shore (27 November 2009)
Series solution of ode: Airy's equation (3 November 2010)
Airy differential equation (26 November 2013)
References
The mathematics of rainbows
Tables of Weyl Fractional Integrals for the Airy Function
Special Functions: An Introduction to the Classical Functions of Mathematical Physics
Airy function zeros