Difference between revisions of "Chi"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| − | The hyperbolic cosine integral $\mathrm{Chi} \ | + | The hyperbolic cosine integral $\mathrm{Chi}$ is defined for $|\mathrm{arg}(z)| < \pi$ the formula |
| − | $$\mathrm{Chi}(z)= | + | $$\mathrm{Chi}(z)=\gamma + \log(z) + \displaystyle\int_0^z \dfrac{\cosh(t)-1}{t} \mathrm{d}t,$$ |
| − | where $\cosh$ denotes the [[cosh|hyperbolic cosine]]. | + | where $\gamma$ denotes the [[Euler-Mascheroni constant]], $\log$ denotes the [[logarithm]], and $\cosh$ denotes the [[cosh|hyperbolic cosine]]. |
<div align="center"> | <div align="center"> | ||
Latest revision as of 23:57, 10 December 2016
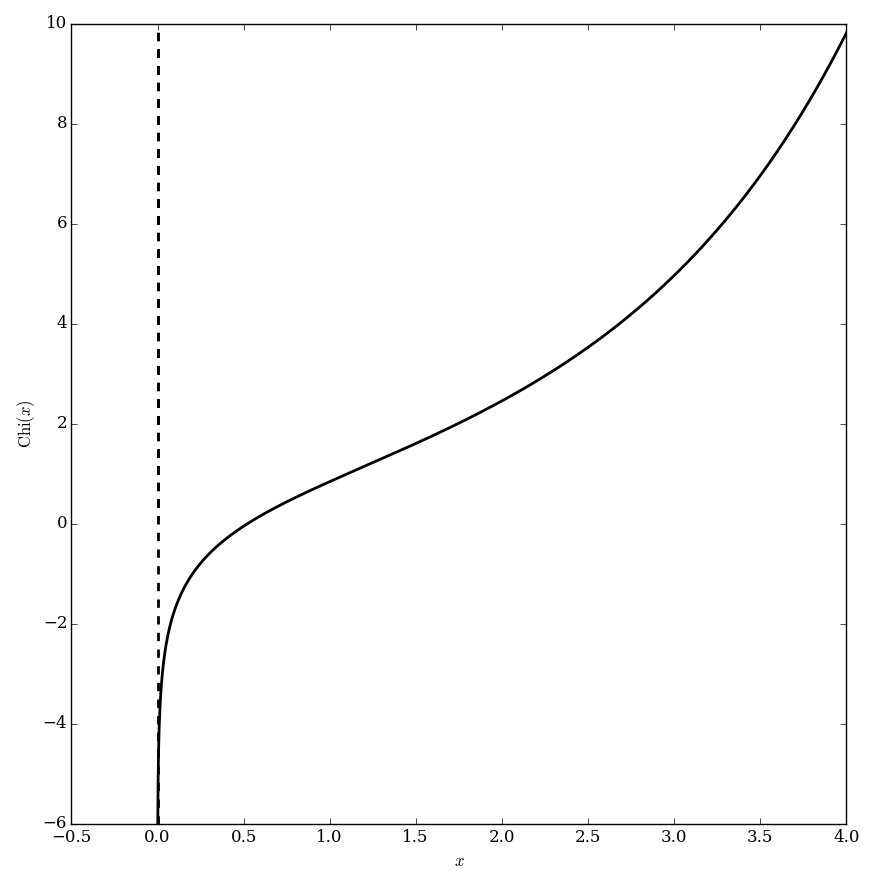
The hyperbolic cosine integral $\mathrm{Chi}$ is defined for $|\mathrm{arg}(z)| < \pi$ the formula $$\mathrm{Chi}(z)=\gamma + \log(z) + \displaystyle\int_0^z \dfrac{\cosh(t)-1}{t} \mathrm{d}t,$$ where $\gamma$ denotes the Euler-Mascheroni constant, $\log$ denotes the logarithm, and $\cosh$ denotes the hyperbolic cosine.
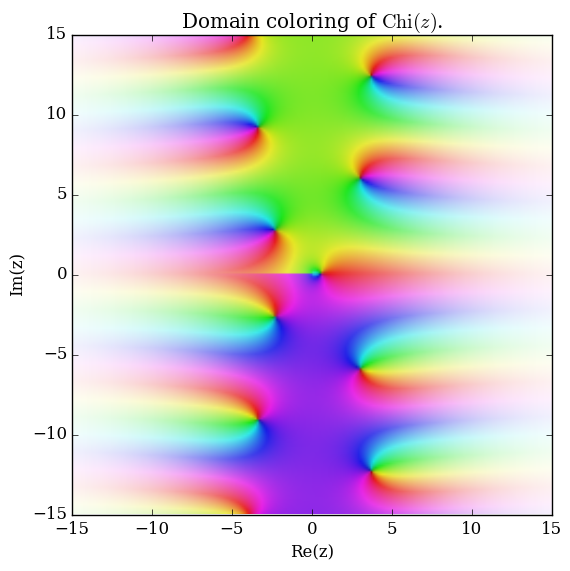
Domain coloring of $\mathrm{Chi}$.
Properties
Derivative of chi
Antiderivative of chi