Difference between revisions of "Triangular numbers"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| − | The triangular numbers $ | + | The triangular numbers $T(n)$ are defined by the formula |
| + | $$T(n)=\displaystyle\sum_{k=1}^n k.$$ | ||
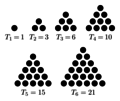
| + | They represent the number of ways to draw an equilateral triangle as in the image below. | ||
<div align="center"> | <div align="center"> | ||
| Line 8: | Line 10: | ||
=Properties= | =Properties= | ||
| + | [[T(n) equals n(n+1)/2]]<br > | ||
| + | [[T(n+1)=T(n)+n+1]]<br /> | ||
| + | [[n^2=T(n)+T(n-1)]]<br /> | ||
| + | [[T(n)^2=T(T(n))+T(T(n-1))]]<br /> | ||
=References= | =References= | ||
Revision as of 01:17, 30 May 2017
The triangular numbers $T(n)$ are defined by the formula $$T(n)=\displaystyle\sum_{k=1}^n k.$$ They represent the number of ways to draw an equilateral triangle as in the image below.
Properties
T(n) equals n(n+1)/2
T(n+1)=T(n)+n+1
n^2=T(n)+T(n-1)
T(n)^2=T(T(n))+T(T(n-1))