Difference between revisions of "Triangular numbers"
From specialfunctionswiki
(→Properties) |
|||
| Line 14: | Line 14: | ||
[[n^2=T(n)+T(n-1)]]<br /> | [[n^2=T(n)+T(n-1)]]<br /> | ||
[[T(n)^2=T(T(n))+T(T(n)-1)]]<br /> | [[T(n)^2=T(T(n))+T(T(n)-1)]]<br /> | ||
| + | [[T(n+1)^2-T(n)^2=(n+1)^3]]<br /> | ||
=References= | =References= | ||
Latest revision as of 01:32, 30 May 2017
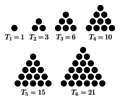
The triangular numbers $T(n)$ are defined for $n=1,2,3,\ldots$ by the formula $$T(n)=\displaystyle\sum_{k=1}^n k.$$ They represent the number of ways to draw an equilateral triangle as in the image below.
Properties
T(n)=n(n+1)/2
T(n+1)=T(n)+n+1
n^2=T(n)+T(n-1)
T(n)^2=T(T(n))+T(T(n)-1)
T(n+1)^2-T(n)^2=(n+1)^3
References
- V.E. Hoggatt, Jr and Marjorie Bicknell: Triangular numbers (1974)... (next) $(1.1)$