Difference between revisions of "Riemann zeta"
From specialfunctionswiki
| Line 1: | Line 1: | ||
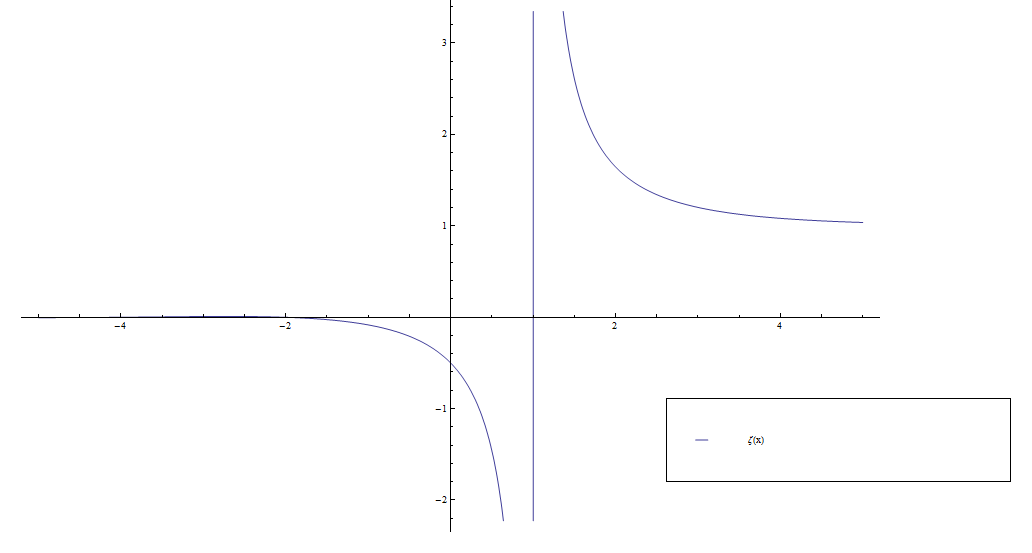
Consider the function $\zeta$ defined by the series | Consider the function $\zeta$ defined by the series | ||
$$\zeta(z) = \displaystyle\sum_{k=0}^{\infty} \dfrac{1}{n^z}.$$ | $$\zeta(z) = \displaystyle\sum_{k=0}^{\infty} \dfrac{1}{n^z}.$$ | ||
| + | |||
| + | [[File:Riemannzeta.png|500px]] | ||
==Properties== | ==Properties== | ||
| Line 19: | Line 21: | ||
=External links= | =External links= | ||
*[https://www.youtube.com/playlist?list=PL32446FDD4DA932C9 15 Videos about the Riemann $\zeta$ function] | *[https://www.youtube.com/playlist?list=PL32446FDD4DA932C9 15 Videos about the Riemann $\zeta$ function] | ||
| + | [http://www.claymath.org/sites/default/files/ezeta.pdf English translation of Riemann's paper "On the number of prime numbers less than a given quantity"] | ||
Revision as of 00:23, 19 October 2014
Consider the function $\zeta$ defined by the series $$\zeta(z) = \displaystyle\sum_{k=0}^{\infty} \dfrac{1}{n^z}.$$
Properties
Proposition: If $\mathrm{Re} \hspace{2pt} z > 1$, then the series defining $\zeta(z)$ converges.
Proof: █
Proposition (Euler Product): $\zeta(z)=\displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z} = \displaystyle\prod_{p \mathrm{\hspace{2pt} prime}} \dfrac{1}{1-p^{-z}}$
Proof: █
External links
English translation of Riemann's paper "On the number of prime numbers less than a given quantity"