Difference between revisions of "Arctanh"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| − | + | ||
| + | <div align="center"> | ||
| + | <gallery> | ||
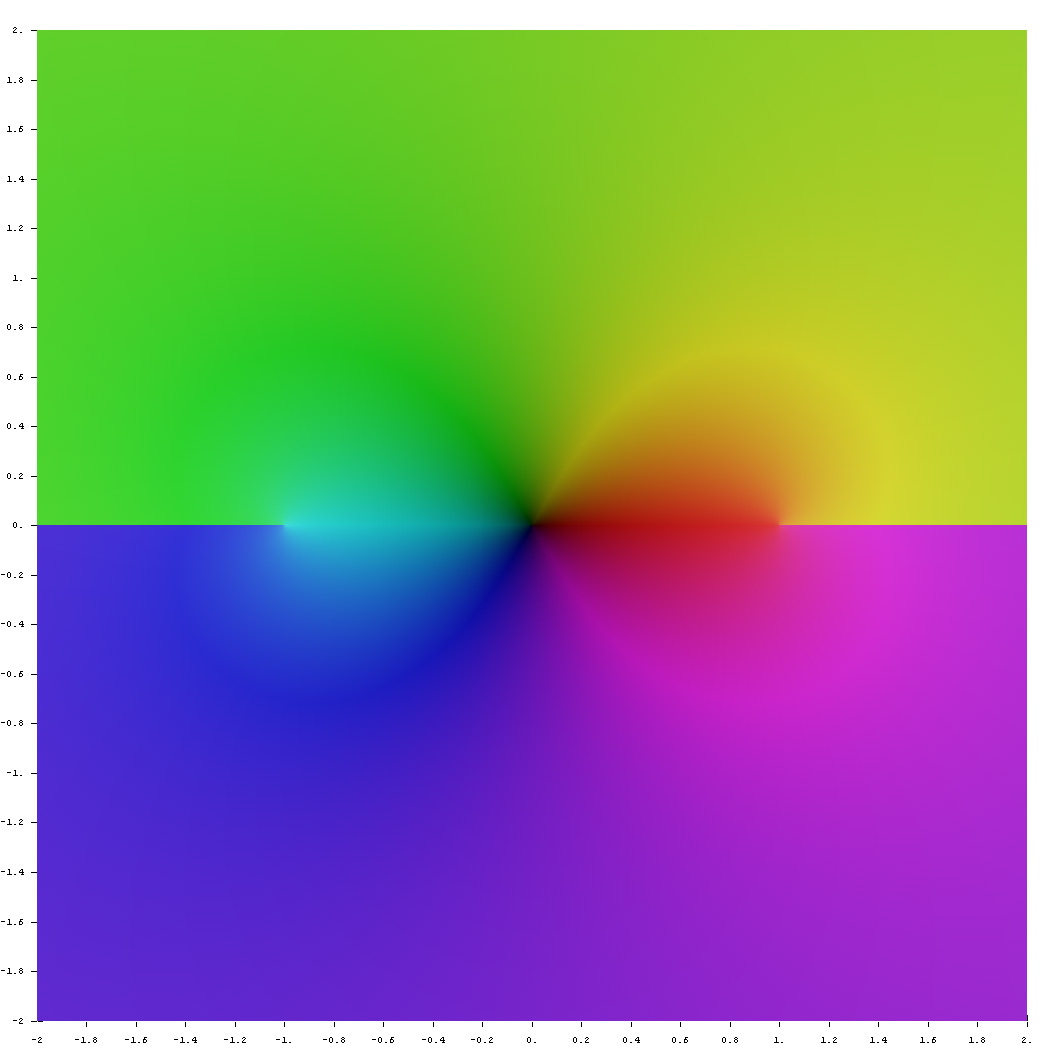
| + | File:Complex ArcTanh.jpg|[[Domain coloring]] of [[analytic continuation]] of $\mathrm{arctanh}$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | {{:Derivative of Legendre chi}} | ||
<center>{{:Inverse hyperbolic trigonometric functions footer}}</center> | <center>{{:Inverse hyperbolic trigonometric functions footer}}</center> | ||
Revision as of 01:33, 21 March 2015
Domain coloring of analytic continuation of $\mathrm{arctanh}$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \chi_2(z) = \dfrac{\mathrm{arctanh}(z)}{z},$$ where $\chi$ denotes the Legendre chi function and $\mathrm{arctanh}$ denotes the inverse hyperbolic tangent function.