Difference between revisions of "Format notes"
From specialfunctionswiki
(→Mathematica code) |
(→Mathematica code) |
||
| Line 34: | Line 34: | ||
=Mathematica code= | =Mathematica code= | ||
| + | ==Domain colorings== | ||
We use the code | We use the code | ||
<pre>ComplexGraph[f_, {xmin_, xmax_}, {ymin_, ymax_}, | <pre>ComplexGraph[f_, {xmin_, xmax_}, {ymin_, ymax_}, | ||
| Line 48: | Line 49: | ||
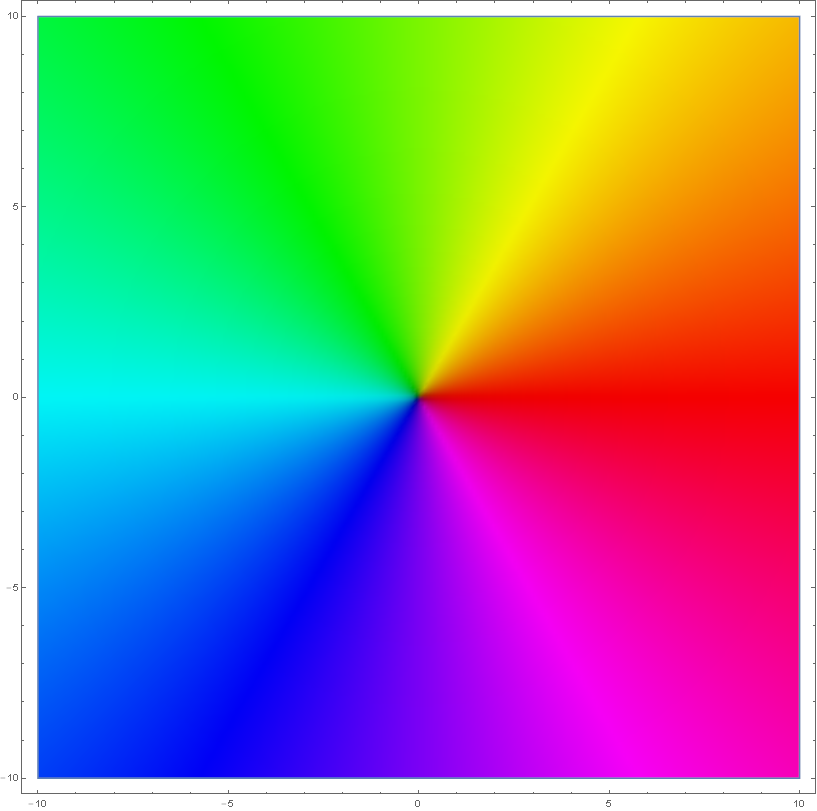
to generate complex domain colorings. This coloring applied to the identity function $f(z)=z$ generates the following picture: | to generate complex domain colorings. This coloring applied to the identity function $f(z)=z$ generates the following picture: | ||
[[File:Complexidentity.png|500px]] | [[File:Complexidentity.png|500px]] | ||
| + | |||
| + | ==Thumbnails== | ||
| + | We use the code | ||
| + | <pre>Plot[AiryAi[x], {x, -12, 3}, PlotStyle -> {Thickness[0.04], Black}, AxesStyle -> Thickness[0.01], Ticks -> None]</pre> | ||
| + | to output the thumbnail | ||
| + | [[File:Airyaithumb.png]] | ||
Revision as of 05:40, 18 May 2015
This is a list of common code templates and styles we use at specialfunctionswiki.
Contents
Theorem/proof box template
The code
<div class="toccolours mw-collapsible mw-collapsed"> <strong>THEOREM/LEMMA/PROPOSITION:</strong> STATEMENT OF THEOREM <div class="mw-collapsible-content"> <strong>Proof:</strong> proof goes here █ </div> </div>
creates
THEOREM/LEMMA/PROPOSITION: STATEMENT OF THEOREM
Proof: proof goes here █
Images
Put images into galleries. Thumbnails and frames break the theorem/proof box template. The code
<div align="center">
<gallery>
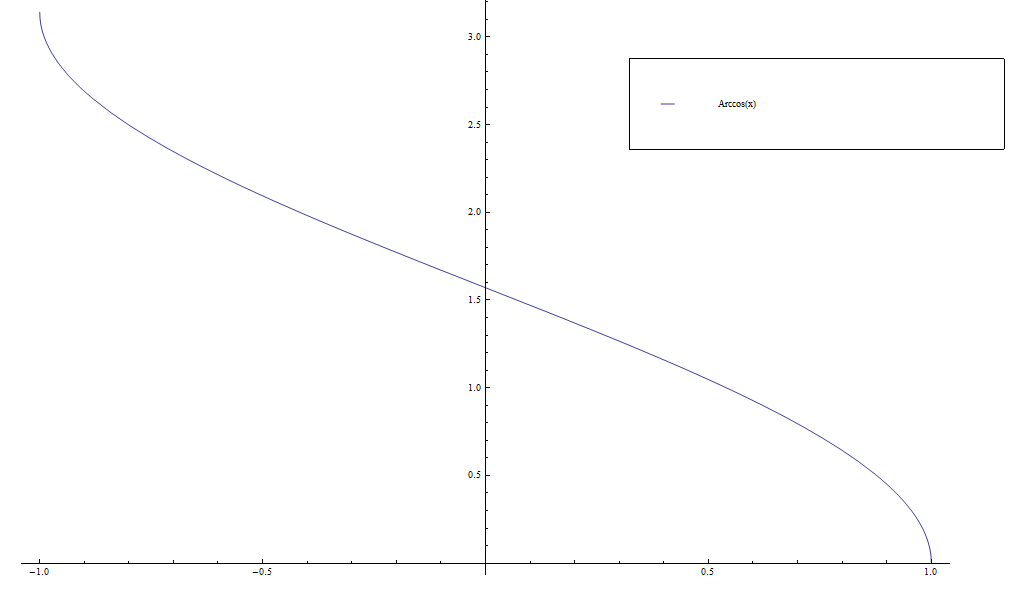
File:Arccos.png|Graph of $\mathrm{arccos}$ on $[-1,1]$.
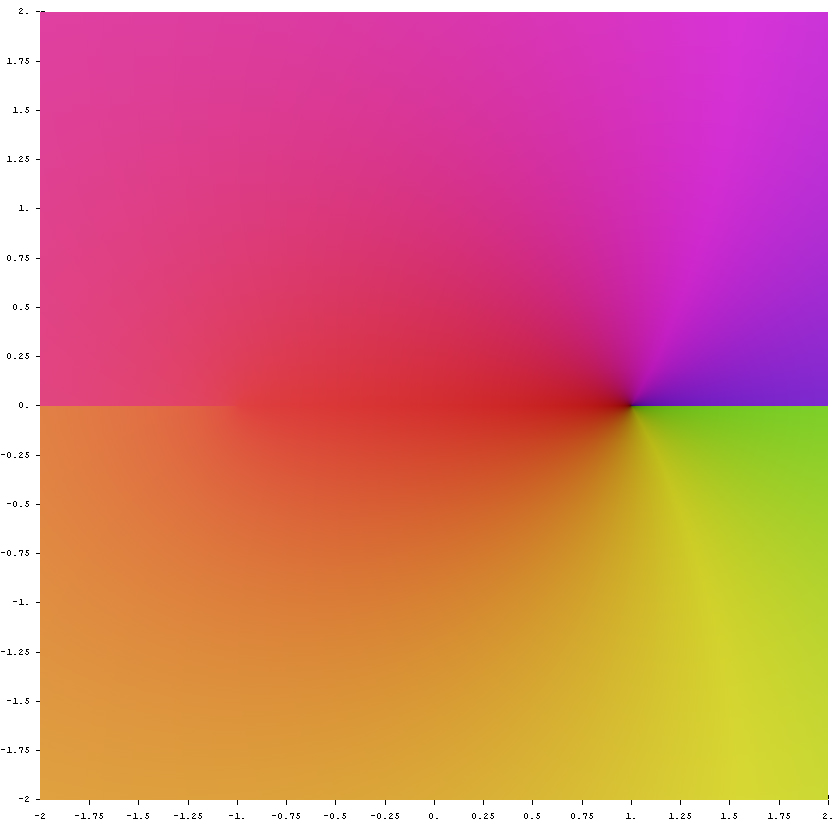
File:Complex arccos.jpg|[[Domain coloring]] of [[analytic continuation]].
</gallery>
</div>
creates
Graph of $\mathrm{arccos}$ on $[-1,1]$.
Mathematica code
Domain colorings
We use the code
ComplexGraph[f_, {xmin_, xmax_}, {ymin_, ymax_},
opts : OptionsPattern[]] :=
RegionPlot[True, {x, xmin, xmax}, {y, ymin, ymax}, opts,
PlotPoints -> 200, ColorFunctionScaling -> False,
ColorFunction ->
Function[{x, y},
With[{ff = f[x + I y]},
ColorConvert[
Hue[(2. Pi)^-1 Mod[Arg[ff], 2 Pi], 1,
1 - (1.2 + 10 Log[Abs[ff] + 1])^-1], "LAB"]]]]
to generate complex domain colorings. This coloring applied to the identity function $f(z)=z$ generates the following picture:
Thumbnails
We use the code
Plot[AiryAi[x], {x, -12, 3}, PlotStyle -> {Thickness[0.04], Black}, AxesStyle -> Thickness[0.01], Ticks -> None]
to output the thumbnail
