Difference between revisions of "Polylogarithm"
From specialfunctionswiki
| Line 8: | Line 8: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Videos= | ||
| + | [https://www.youtube.com/watch?v=6v60ivoC2z8 polylogarithm function] | ||
=Properties= | =Properties= | ||
{{:Lerch transcendent polylogarithm}} | {{:Lerch transcendent polylogarithm}} | ||
{{:Legendre chi in terms of polylogarithm}} | {{:Legendre chi in terms of polylogarithm}} | ||
Revision as of 00:18, 20 May 2015
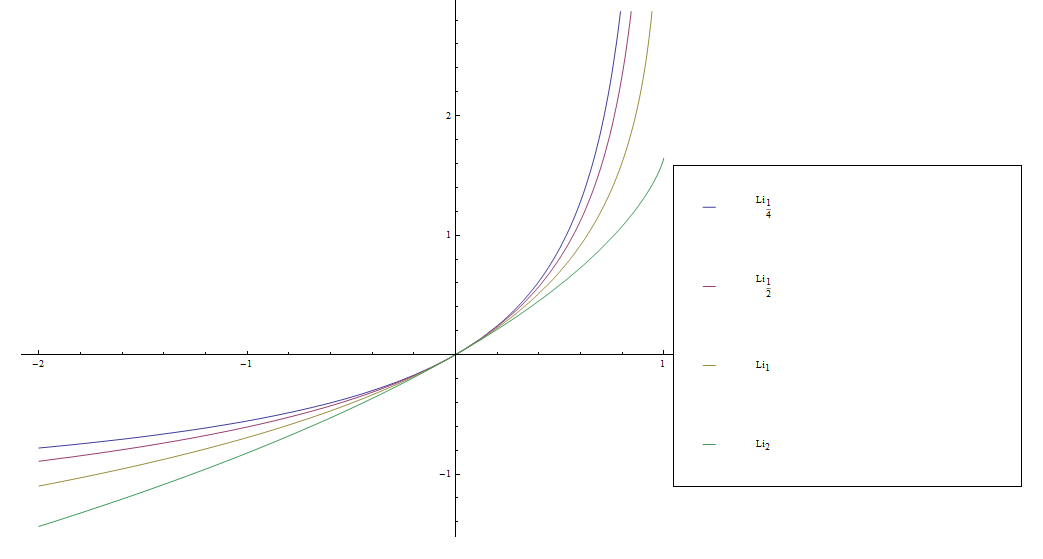
The polylogarithm $\mathrm{Li}_s$ is defined by the formula $$\mathrm{Li}_s(z) = \sum_{k=1}^{\infty} \dfrac{z^k}{k^s} = z + \dfrac{z^2}{2^s} + \dfrac{z^3}{3^s} + \ldots$$ A special case of the polylogarithm with $s=2$ is called a dilogarithm.
Contents
Videos
Properties
Theorem
The following formula holds: $$\Phi(z,n,1)=\dfrac{\mathrm{Li}_n(z)}{z},$$ where $\Phi$ denotes the Lerch transcendent and $\mathrm{Li_n}$ denotes the polylogarithm.
Proof
References
Theorem
The following formula holds: $$\chi_{\nu}(z)=\dfrac{1}{2}[\mathrm{Li}_{\nu}(z)-\mathrm{Li}_{\nu}(-z)] = \mathrm{Li}_{\nu}(z)-2^{-\nu}\mathrm{Li}_{\nu}(z^2),$$ where $\chi$ denotes the Legendre chi function and $\mathrm{Li}_{\nu}$ denotes the polylogarithm.