Difference between revisions of "Modified Bessel I"
(→Properties) |
(→Properties) |
||
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
{{:Relationship between Bessel I sub 1/2 and cosh}} | {{:Relationship between Bessel I sub 1/2 and cosh}} | ||
| + | {{:Relationship between Bessel I sub 1/2 and sinh}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
Revision as of 00:29, 5 July 2015
The modified Bessel function of the first kind is defined by $$I_{\nu}(z)=i^{-\nu}J_{\nu}(iz),$$ where $J_{\nu}$ is the Bessel function of the first kind.
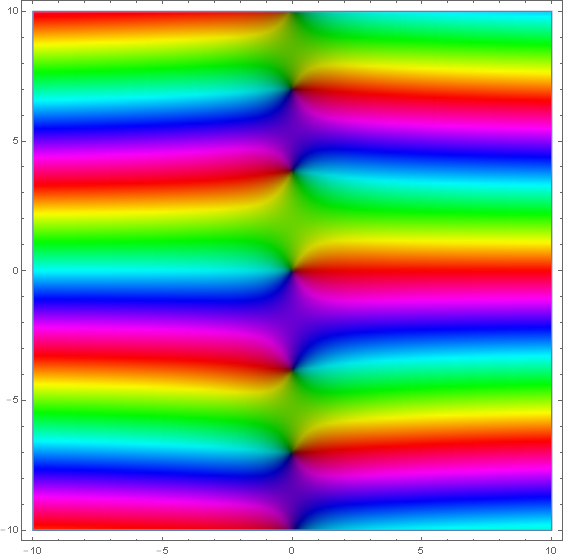
Domain coloring of analytic continuation of $I_1(z)$.
Contents
Properties
Theorem
The following formula holds: $$I_{-\frac{1}{2}}(z)=\sqrt{\dfrac{2}{\pi z}} \cosh(z),$$ where $I_{-\frac{1}{2}}$ denotes the modified Bessel function of the first kind and $\cosh$ denotes the hyperbolic cosine.
Proof
References
Theorem
The following formula holds: $$I_{\frac{1}{2}}(z)=\sqrt{\dfrac{2}{\pi z}}\sinh(z),$$ where $I_{\frac{1}{2}}$ denotes the modified Bessel function of the first kind and $\sinh$ denotes the hyperbolic sine.
Proof
References
Proposition: The following formula holds: $$I_{\nu}(z)=\displaystyle\sum_{k=0}^{\infty} J_{\nu+k}(z) \dfrac{z^k}{k!},$$ where $J_{\nu}$ denotes the Bessel function of the first kind.
Proof: █
Theorem
The following formula holds: $$\mathrm{Bi}(z)=\sqrt{\dfrac{z}{3}} \left( I_{\frac{1}{3}}\left(\frac{2}{3}x^{\frac{3}{2}} \right) + I_{-\frac{1}{3}} \left( \frac{2}{3} x^{\frac{3}{2}} \right) \right),$$ where $\mathrm{Bi}$ denotes the Airy Bi function and $I_{\nu}$ denotes the modified Bessel $I$.