Difference between revisions of "Elliptic E"
From specialfunctionswiki
| Line 6: | Line 6: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
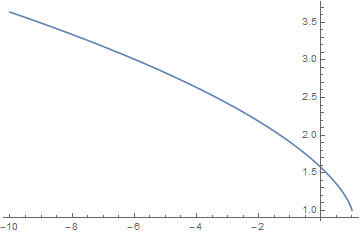
| + | File:Elliptice plot.png|Plot of $E(m)$ on $[-10,1]$. | ||
File:Domaincoloringelliptice.png|[[Domain coloring]] of $E(m)$. | File:Domaincoloringelliptice.png|[[Domain coloring]] of $E(m)$. | ||
</gallery> | </gallery> | ||
Revision as of 18:05, 25 July 2015
If $m=k^2$ we define the complete elliptic integral of the second kind, $E$, to be $$E(k)=E(m)=\displaystyle\int_0^{\frac{\pi}{2}} \sqrt{1-k^2\sin^2 \theta} d\theta.$$ The incomplete elliptic integral of the second kind is $$E(\phi|k)=E(\phi|m)=\displaystyle\int_0^{\phi} \sqrt{1-m\sin^2 \theta}d\theta.$$
- Domaincoloringelliptice.png
Domain coloring of $E(m)$.