Difference between revisions of "Shi"
From specialfunctionswiki
| Line 1: | Line 1: | ||
The hyperbolic sine integral is defined by the formula | The hyperbolic sine integral is defined by the formula | ||
$$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} dt.$$ | $$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} dt.$$ | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
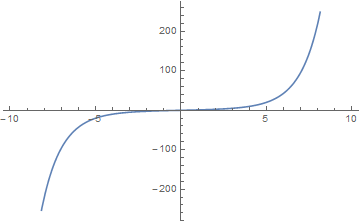
| + | File:Plot of hyperbolic sinh integral.png|Plot of $\mathrm{Shi}$ on $[-10,10]$. | ||
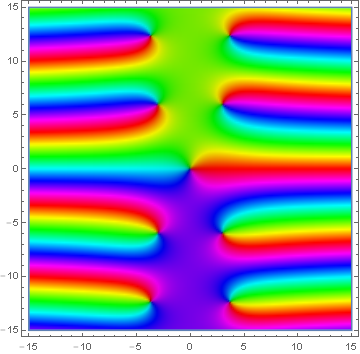
| + | File:Domain coloring hyperbolic sine integral.png | ||
| + | |[[Domain coloring]] of [[analytic continuation]] of $\mathrm{Shi}$. | ||
| + | </gallery> | ||
| + | </div> | ||
<center>{{:*-integral functions footer}}</center> | <center>{{:*-integral functions footer}}</center> | ||
Revision as of 18:46, 25 July 2015
The hyperbolic sine integral is defined by the formula $$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} dt.$$