Difference between revisions of "Coth"
| Line 12: | Line 12: | ||
{{:Derivative of coth}} | {{:Derivative of coth}} | ||
{{:Antiderivative of coth}} | {{:Antiderivative of coth}} | ||
| + | {{:Taylor series of coth}} | ||
{{:Relationship between coth and cot}} | {{:Relationship between coth and cot}} | ||
{{:Relationship between cot and coth}} | {{:Relationship between cot and coth}} | ||
<center>{{:Hyperbolic trigonometric functions footer}}</center> | <center>{{:Hyperbolic trigonometric functions footer}}</center> | ||
Revision as of 18:57, 25 August 2015
The hyperbolic cotangent is defined by $$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)},$$ where $\tanh$ denotes the hyperbolic tangent function.
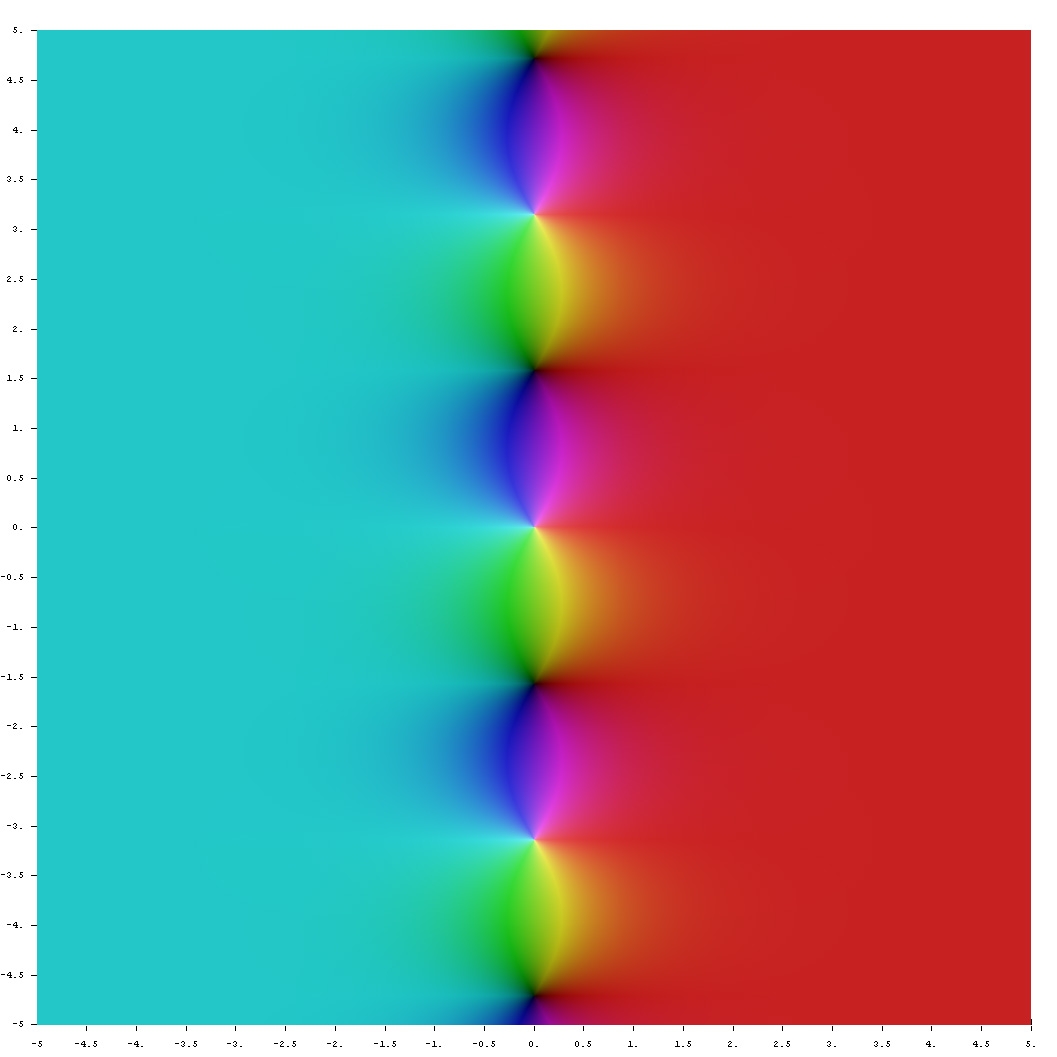
Domain coloring of $\mathrm{coth}$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{coth}(z) = -\mathrm{csch}^2(z),$$ where $\mathrm{coth}$ denotes the hyperbolic cotangent and $\mathrm{csch}$ denotes the hyperbolic cosecant.
Proof
By the definition, $$\mathrm{coth}(z) = \dfrac{\mathrm{cosh}(z)}{\mathrm{sinh}(z)}.$$ Using the quotient rule, the derivative of sinh, the derivative of cosh, Pythagorean identity for sinh and cosh, and the definition of $\mathrm{csch}$, we see $$\begin{array}{ll} \dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{coth}(z) &= \dfrac{\sinh^2(z)-\cosh^2(z)}{\mathrm{sinh}^2(z)} \\ &= - \dfrac{\mathrm{cosh}^2(z)-\mathrm{sinh}^2(z)}{\mathrm{sinh}^2(z)} \\ &= -\mathrm{csch}^2(z), \end{array}$$ as was to be shown.
References
Theorem
The following formula holds: $$\displaystyle\int \mathrm{coth}(z) \mathrm{d}z=\log(\sinh(z)) + C,$$ for arbitrary constant $C$, where $\mathrm{coth}$ denotes the hyperbolic cotangent, $\log$ denotes the logarithm, and $\sinh$ denotes the hyperbolic sine.
Proof
By definition, $$\mathrm{coth}(z) = \dfrac{\mathrm{cosh}(z)}{\mathrm{sinh}(z)}.$$ Let $u=\mathrm{sinh}(z)$ and use the derivative of sinh, u-substitution, and the definition of the logarithm to derive $$\begin{array}{ll} \displaystyle\int \mathrm{coth}(z) \mathrm{d}z &= \displaystyle\int \dfrac{1}{u} \mathrm{d} u \\ &= \log \left( \mathrm{sinh}(z) \right) + C, \end{array}$$ as was to be shown. █
References
Taylor series of cothTheorem
The following formula holds: $$\coth(z)=i\cot(iz),$$ where $\coth$ denotes the hyperbolic cotangent and $\cot$ denotes the cotangent.
Proof
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.5.12$
Theorem
The following formula holds: $$\cot(z)=i\coth(iz),$$ where $\cot$ denotes the cotangent and $\coth$ denotes the hyperbolic cotangent.