Difference between revisions of "Inverse Gudermannian"
| Line 16: | Line 16: | ||
{{:Relationship between csch, inverse Gudermannian, and cot}} | {{:Relationship between csch, inverse Gudermannian, and cot}} | ||
{{:Relationship between sech, inverse Gudermannian, and cos}} | {{:Relationship between sech, inverse Gudermannian, and cos}} | ||
| − | + | {{:Relationship between coth, inverse Gudermannian, and csc}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<center>{{:*-integral functions footer}}</center> | <center>{{:*-integral functions footer}}</center> | ||
Revision as of 23:37, 25 August 2015
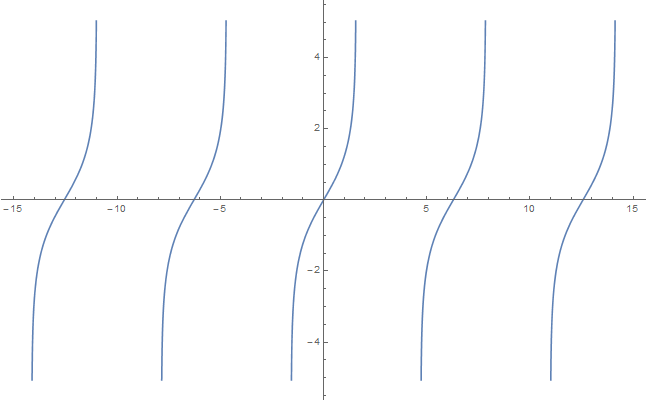
The inverse Gudermannian $\mathrm{gd}^{-1}$ is the inverse function of the Gudermannian function. It may be defined by the following formula for $x \in \mathbb{R}$: $$\mathrm{gd}^{-1}(x)=\displaystyle\int_0^x \dfrac{1}{\cosh(t)} dt,$$ where $\cosh$ denotes the hyperbolic cosine.
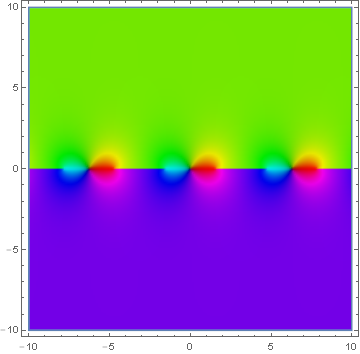
Domain coloring of $\mathrm{gd}^{-1}$.
Contents
Properties
Theorem
The following formula holds: $$\sinh(\mathrm{gd}^{-1}(x))=\tan(x),$$ where $\sinh$ is the hyperbolic sine, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\tan$ is the tangent.
Proof
References
Theorem
The following formula holds: $$\cosh(\mathrm{gd}^{-1}(x))=\sec(x),$$ where $\cosh$ is the hyperbolic cosine, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\sec$ is the secant.
Proof
References
Theorem
The following formula holds: $$\mathrm{tanh}(\mathrm{gd}^{-1}(x))=\sin(x),$$ where $\mathrm{tanh}$ denotes the hyperbolic tangent, $\mathrm{gd}^{-1}$ denotes the inverse Gudermannian, and $\sin$ denotes sine.
Proof
References
Theorem
The following formula holds: $$\mathrm{csch}(\mathrm{gd}^{-1}(x))=\cot(x),$$ where $\mathrm{csch}$ is the hyperbolic cosecant, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\cot$ is the cotangent.
Proof
References
Theorem
The following formula holds: $$\mathrm{sech}(\mathrm{gd}^{-1}(x))=\cos(x),$$ where $\mathrm{sech}$ is the hyperbolic secant, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\cos$ is the cosine.
Proof
References
Theorem
The following formula holds: $$\mathrm{coth}(\mathrm{gd}^{-1}(x))=\csc(x),$$ where $\mathrm{coth}$ is the hyperbolic cotangent, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\csc$ is the cosecant.