Difference between revisions of "Arcsinh"
From specialfunctionswiki
| Line 17: | Line 17: | ||
</div> | </div> | ||
</div> | </div> | ||
| + | |||
| + | =References= | ||
| + | [http://dualaud.net/specialfunctionswiki/abramowitz_and_stegun-1.03/page_86.htm Abramowitz&Stegun] | ||
<center>{{:Inverse hyperbolic trigonometric functions footer}}</center> | <center>{{:Inverse hyperbolic trigonometric functions footer}}</center> | ||
Revision as of 09:35, 9 November 2015
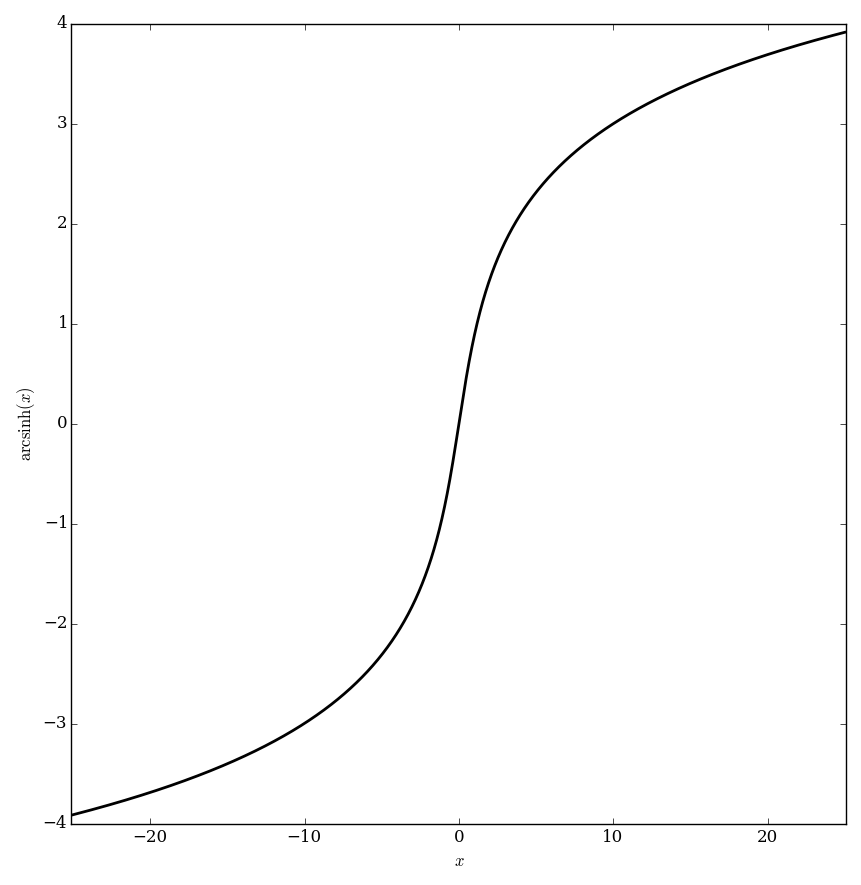
The $\mathrm{arcsinh}$ function is the inverse function of the hyperbolic sine function defined by $$\mathrm{arcsinh}(z)=\log\left(z+\sqrt{1+z^2}\right).$$
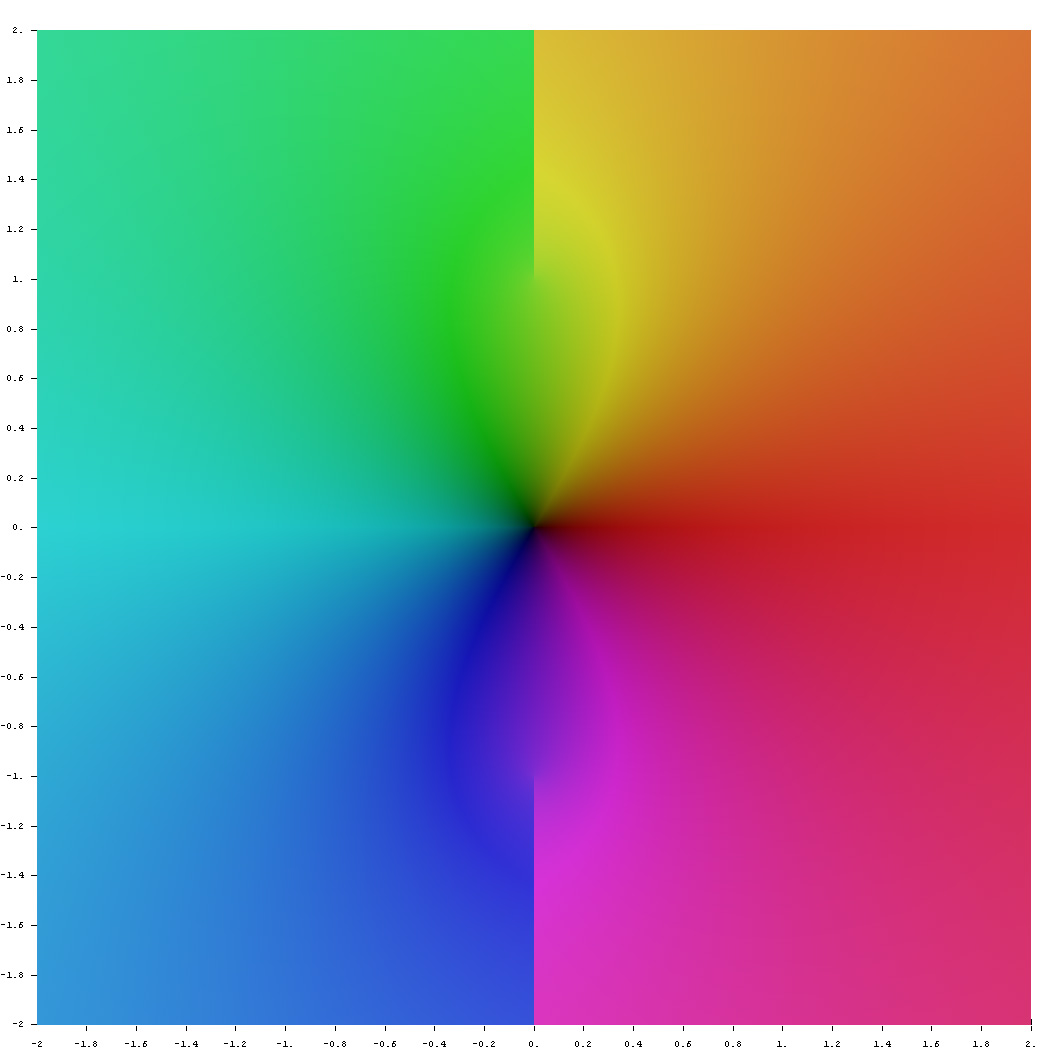
Domain coloring of analytic continuation of $\mathrm{arcsinh}$.
Properties
Theorem: The following formula holds: $$\dfrac{d}{dz} \mathrm{arcsinh}(z) = \dfrac{1}{\sqrt{1+z^2}}.$$
Proof: █