Difference between revisions of "Cotangent"
| Line 5: | Line 5: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
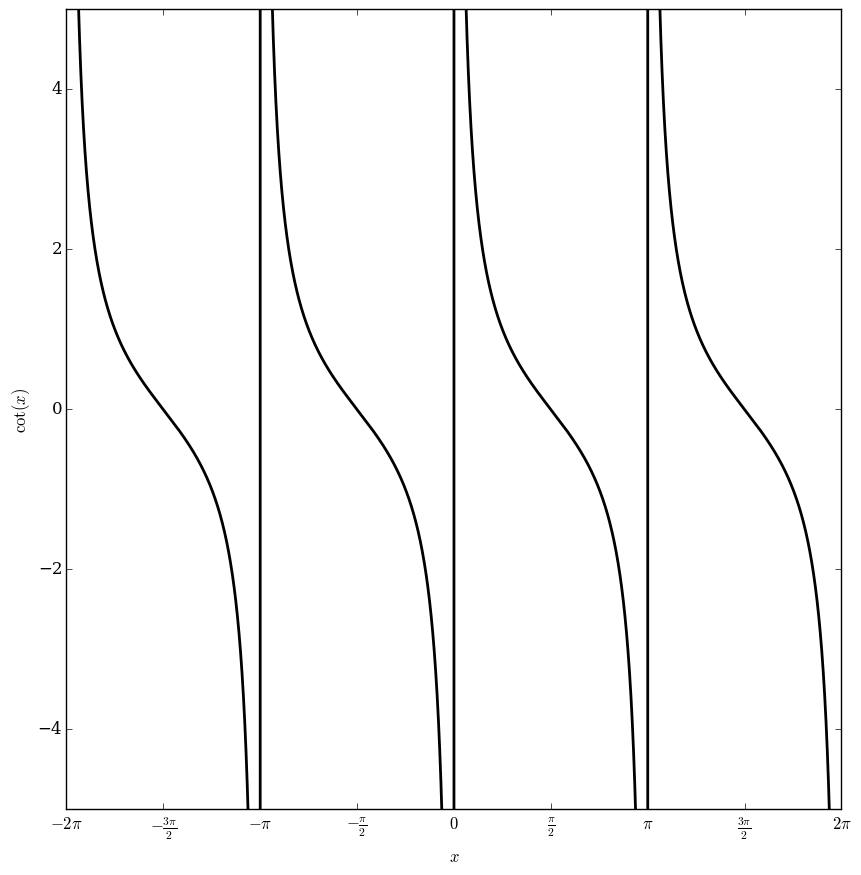
| − | File: | + | File:Cotangentplot.png|Plot of cotangent function over $[-2\pi,2\pi]$. |
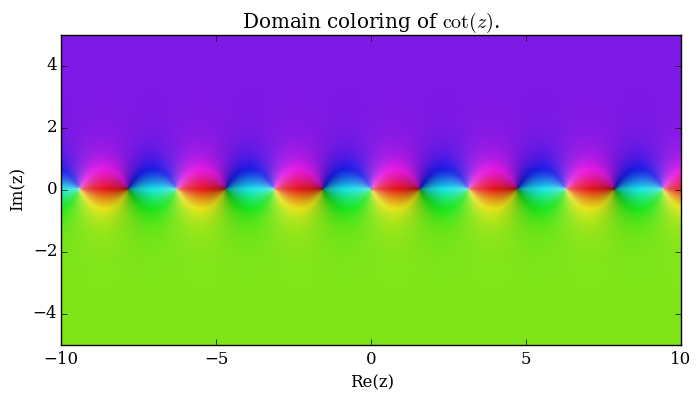
File:Complexcotangentplot.png|[[Domain coloring]] of $\cot$. | File:Complexcotangentplot.png|[[Domain coloring]] of $\cot$. | ||
</gallery> | </gallery> | ||
Revision as of 05:08, 8 February 2016
The cotangent function is defined by the formula $$\cot(z)=\dfrac{1}{\tan z} \equiv \dfrac{\cos(z)}{\sin(z)},$$ where $\tan$ denotes the tangent function.
Domain coloring of $\cot$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z}\cot(z)=-\csc^2(z),$$ where $\cot$ denotes the cotangent and $\csc$ denotes the cosecant.
Proof
Apply the quotient rule to the definition of cotangent using derivative of sine and derivative of cosine to see $$\begin{array}{ll} \dfrac{\mathrm{d}}{\mathrm{d}z} \cot(z) &= \dfrac{\mathrm{d}}{\mathrm{d}x} \left[ \dfrac{\cos(z)}{\sin(z)} \right] \\ &= \dfrac{-\sin^2(z)-\cos^2(z)}{\sin^2(z)} \\ &= -\dfrac{\sin^2(z)+\cos^2(z)}{\sin^2(z)}. \end{array}$$ Now apply the Pythagorean identity for sin and cos and the definition of cosecant to see $$\dfrac{\mathrm{d}}{\mathrm{d}z} \cot(z) = -\dfrac{1}{\sin^2(z)} = -\csc^2(z),$$ as was to be shown. █
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.3.110$
Theorem
The following formula holds: $$\cot(z)=i\coth(iz),$$ where $\cot$ denotes the cotangent and $\coth$ denotes the hyperbolic cotangent.
Proof
References
Theorem
The following formula holds: $$\coth(z)=i\cot(iz),$$ where $\coth$ denotes the hyperbolic cotangent and $\cot$ denotes the cotangent.
Proof
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.5.12$
Theorem
The following formula holds: $$\cot(\mathrm{gd}(x))=\mathrm{csch}(x),$$ where $\cot$ is the cotangent, $\mathrm{gd}$ is the Gudermannian, and $\mathrm{csch}$ is the hyperbolic cosecant.
Proof
References
Theorem
The following formula holds: $$\mathrm{csch}(\mathrm{gd}^{-1}(x))=\cot(x),$$ where $\mathrm{csch}$ is the hyperbolic cosecant, $\mathrm{gd}^{-1}$ is the inverse Gudermannian, and $\cot$ is the cotangent.