Difference between revisions of "Arctan"
(→Properties) |
|||
| Line 9: | Line 9: | ||
=Properties= | =Properties= | ||
| − | + | {{:Derivative of arctan}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
Revision as of 03:27, 16 May 2016
The $\mathrm{arctan}$ function is the inverse function of the tangent function.
- Arctan.png
Graph of $\mathrm{arctan}$ on $[-1,1]$.
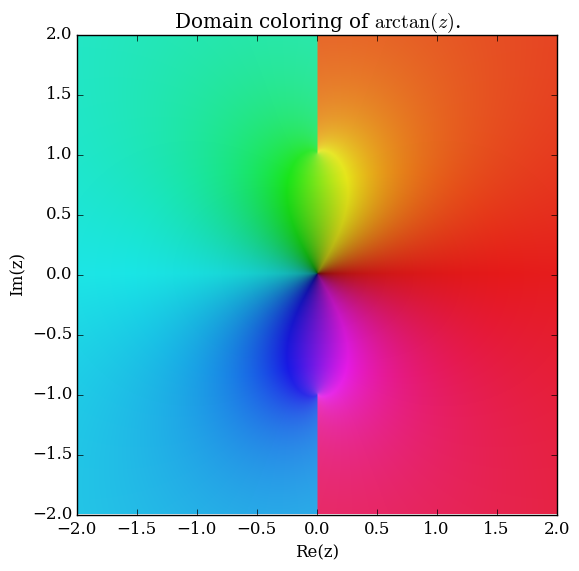
Domain coloring of $\mathrm{arctan}$ on $[-2,2] \times [-2,2] \subset \mathbb{C}.$
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arctan}(z) = \dfrac{1}{z^2+1},$$ where $\mathrm{arctan}$ denotes the inverse tangent function.
Proof
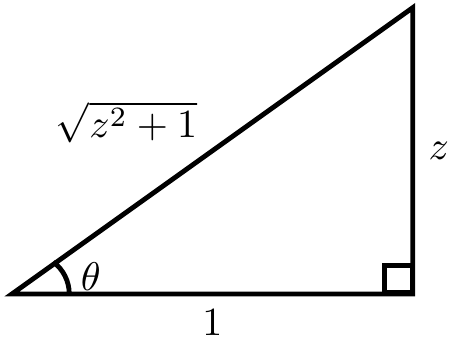
If $\theta=\mathrm{arctan}(z)$ then $\tan \theta = z$. Now implicit differentiation with respect to $z$ yields $$\sec^2(\theta)\theta'=1.$$ The following triangle shows that $\sec^2(\mathrm{arctan}(z))=z^2+1$:
Substituting back in $\theta=\mathrm{arccos(z)}$ yields the formula $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arccos(z)} = \dfrac{1}{\sec^2(\mathrm{arctan(z)})} = \dfrac{1}{z^2+1},$$ as was to be shown. █
References
Proposition: $\displaystyle\int \mathrm{arctan}(z) = z\mathrm{arctan}(z) - \dfrac{1}{2}\log(1+z^2)+C$
Proof: █
Proposition: $\mathrm{arctan}(z) = \mathrm{arccot}\left( \dfrac{1}{z} \right)$
Proof: █
Relationship between arctan and hypergeometric 2F1