Difference between revisions of "Arccot"
| Line 1: | Line 1: | ||
| − | + | The [[function]] $\mathrm{arccot} \colon \mathbb{R} \rightarrow \left( - \dfrac{\pi}{2}, \dfrac{\pi}{2} \right] \setminus \{0\}$ is the [[inverse function]] of the [[cotangent]] function. | |
<div align="center"> | <div align="center"> | ||
Revision as of 05:35, 16 May 2016
The function $\mathrm{arccot} \colon \mathbb{R} \rightarrow \left( - \dfrac{\pi}{2}, \dfrac{\pi}{2} \right] \setminus \{0\}$ is the inverse function of the cotangent function.
- Arccots.png
Graph of $\mathrm{arccot}_1$ and $\mathrm{arccot}_2$ on $\mathbb{R}$.
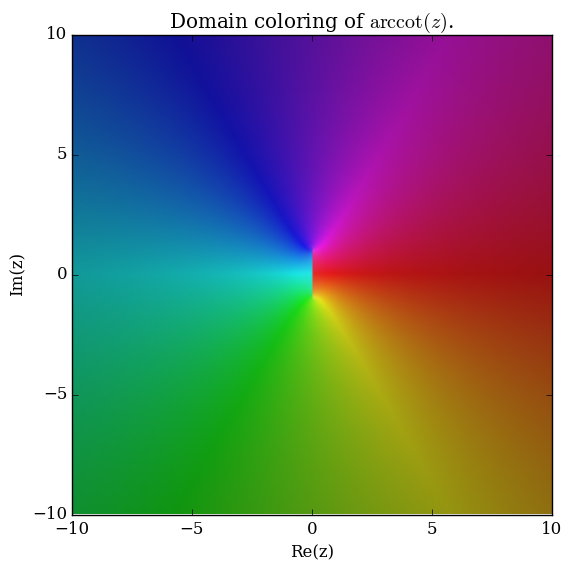
Domain coloring of $\mathrm{arccot}$.
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arccot}(z) = -\dfrac{1}{z^2+1},$$ where $\mathrm{arccot}$ denotes the inverse cotangent function.
Proof
If $y=\mathrm{arccot}(z)$ then $\cot(y)=z$. Now use implicit differentiation with respect to $z$ to get $$-\csc^2(y)y'=1.$$ Substituting back in $y=\mathrm{arccos}(z)$ yields the formula $$\dfrac{\mathrm{d}}{\mathrm{d}z} \mathrm{arccot}(z) = -\dfrac{1}{\csc^2(\mathrm{arccot}(z))} = -\dfrac{1}{z^2+1},$$ as was to be shown. █
References
References
Which is the correct graph of arccot x?