Difference between revisions of "Shi"
From specialfunctionswiki
m (Tom moved page Hyperbolic sine integral to Shi) |
|||
| Line 1: | Line 1: | ||
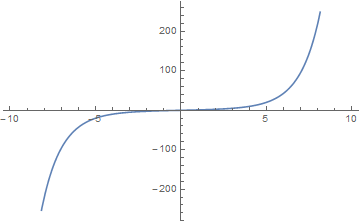
The hyperbolic sine integral is defined by the formula | The hyperbolic sine integral is defined by the formula | ||
| − | $$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} | + | $$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} \mathrm{d}t.$$ |
<div align="center"> | <div align="center"> | ||
Revision as of 22:03, 23 May 2016
The hyperbolic sine integral is defined by the formula $$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} \mathrm{d}t.$$
Plot of $\mathrm{Shi}$ on $[-10,10]$.
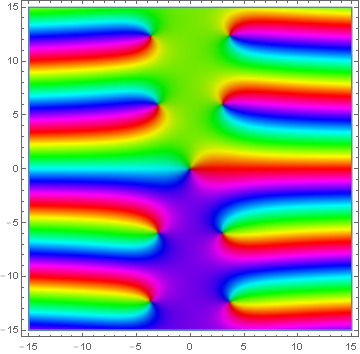
Domain coloring of analytic continuation of $\mathrm{Shi}$.
