Difference between revisions of "Reciprocal gamma"
From specialfunctionswiki
(→Properties) |
|||
| Line 12: | Line 12: | ||
=Properties= | =Properties= | ||
{{:Gamma function Weierstrass product}} | {{:Gamma function Weierstrass product}} | ||
| + | {{:Contour integral representation of reciprocal gamma}} | ||
=See Also= | =See Also= | ||
[[Gamma function]] <br /> | [[Gamma function]] <br /> | ||
Revision as of 00:32, 24 May 2016
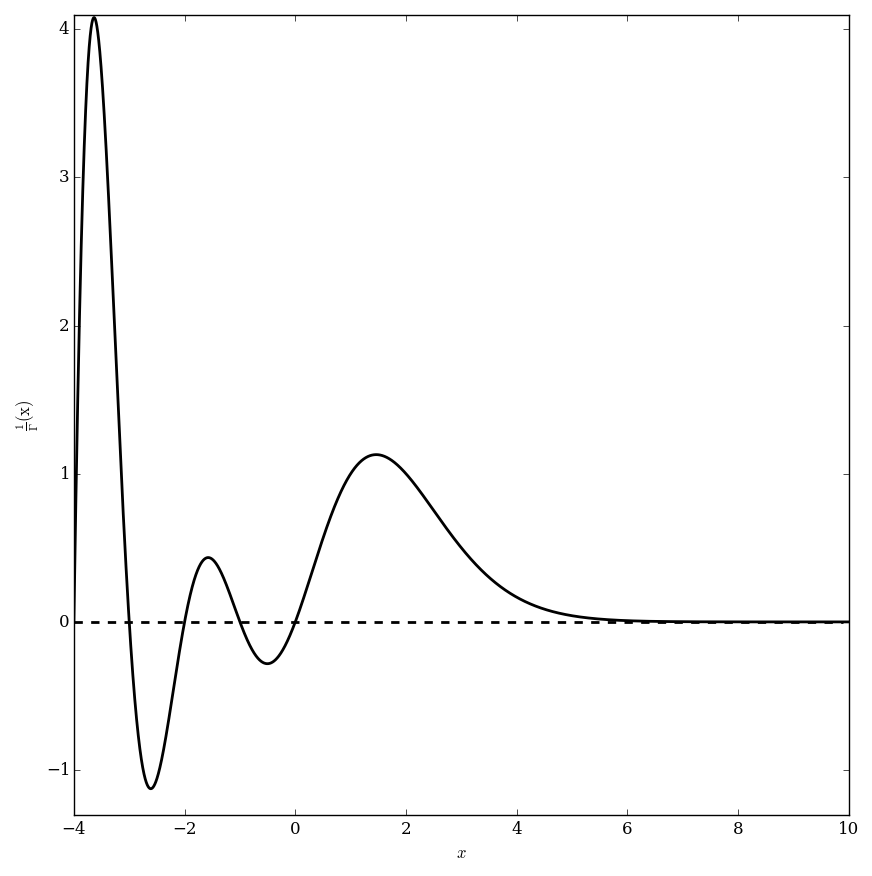
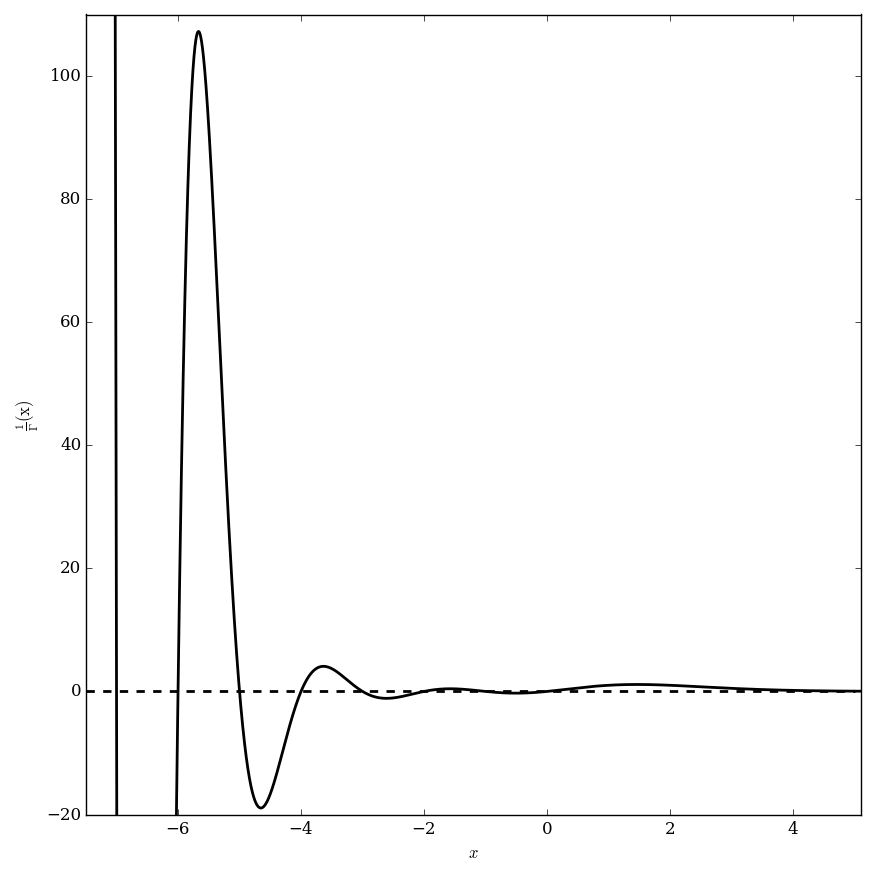
The reciprocal gamma function is the function $\dfrac{1}{\Gamma(z)}$, where $\Gamma$ denotes the gamma function.
Graph of $\dfrac{1}{\Gamma}$ on $[-4,10]$.
Graph of $\dfrac{1}{\Gamma}$ on $[-7.5,5.1]$.
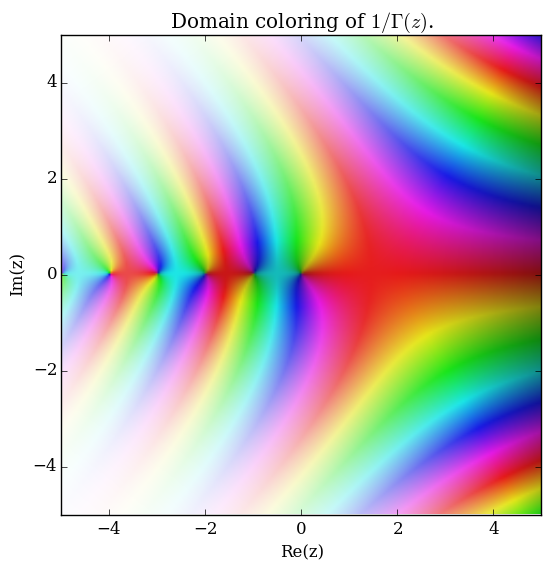
Domain coloring of $\dfrac{1}{\Gamma}$.
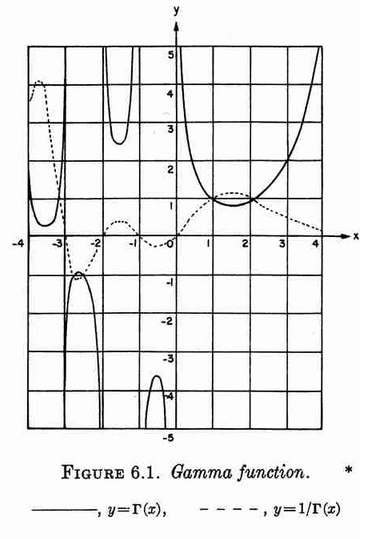
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
.png)
Properties
Gamma function Weierstrass product
Theorem
The following formula holds for a positively oriented contour $C$ is a path encircling $0$ beginning at and returning to $+\infty$: $$\dfrac{1}{\Gamma(z)} = \dfrac{i}{2\pi} \displaystyle\oint_C (-t)^{-z}e^{-t} \mathrm{d}t,$$ where $\dfrac{1}{\Gamma}$ denotes the reciprocal gamma function, $\pi$ denotes pi, and $e^{-t}$ denotes the exponential function.
