Difference between revisions of "Dirichlet eta"
From specialfunctionswiki
| Line 12: | Line 12: | ||
=See Also= | =See Also= | ||
[[Riemann zeta]]<br /> | [[Riemann zeta]]<br /> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:26, 24 May 2016
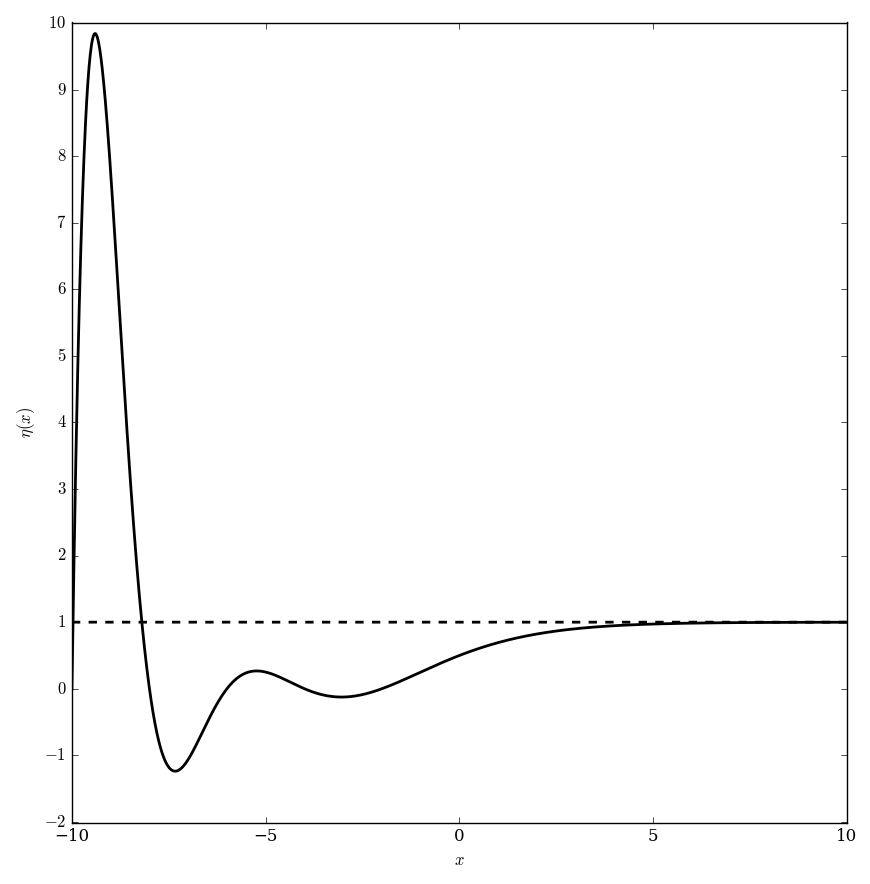
Let $\mathrm{Re} \hspace{2pt} z > 0$, then define $$\eta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n^s}.$$ This series is clearly the Riemann zeta function with alternating terms.
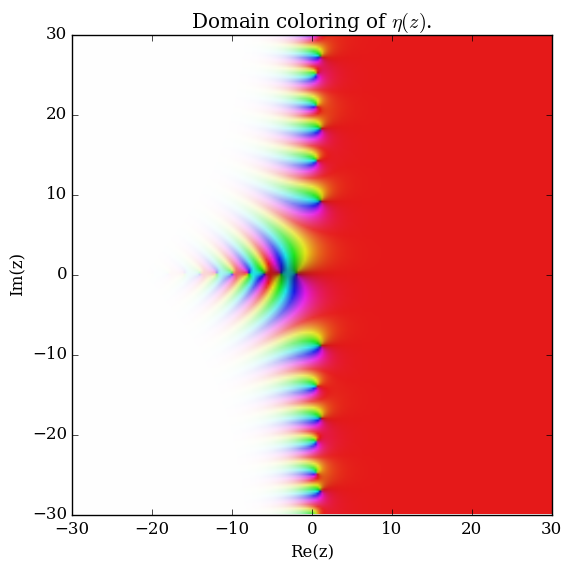
Domain coloring of $\eta$.